题目内容
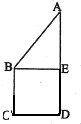 (2012•安庆二模)如图正方形BCDE的边长为a,已知AB=
(2012•安庆二模)如图正方形BCDE的边长为a,已知AB=| 3 |
(1)AB与DE所成角的正切值是
| 2 |
(2)VB-ACE的体积是
| 1 |
| 6 |
(3)AB∥CD;
(4)平面EAB⊥平面ADE;
(5)直线BA与平面ADE所成角的正弦值为
| ||
| 3 |
其中正确的叙述有
(1)(2)(4)(5)
(1)(2)(4)(5)
(写出所有正确结论的编号).分析:(1)由于BC∥DE,则∠ABC(或其补角)为AB与DE所成角;
(2)VB-ACE的体积是
S△BCE×AD=
×
×a×a×a=
a2;
(3)根据CD∥BE,可知AB与CD不平行;
(4)证明BE⊥平面ADE,利用面面平行的判定,可得平面EAB⊥平面ADE;
(5)确定∠BAE为直线BA与平面ADE所成角,即可求解.
(2)VB-ACE的体积是
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 6 |
(3)根据CD∥BE,可知AB与CD不平行;
(4)证明BE⊥平面ADE,利用面面平行的判定,可得平面EAB⊥平面ADE;
(5)确定∠BAE为直线BA与平面ADE所成角,即可求解.
解答: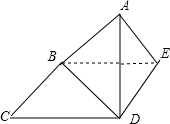 解:由题意,AD⊥平面BCDE,AD=a,AC=
解:由题意,AD⊥平面BCDE,AD=a,AC=
a
(1)由于BC∥DE,∴∠ABC(或其补角)为AB与DE所成角
∵AB=
a,BC=a,AC=
a,∴BC⊥AC,∴tan∠ABC=
,故(1)正确;
(2)VB-ACE的体积是
S△BCE×AD=
×
×a×a×a=
a2,故(2)正确;
(3)∵CD∥BE,∴AB与CD不平行,故(3)不正确;
(4)∵AD⊥平面BCDE,BE?平面BCDE,∴AD⊥BE,∵BE⊥ED,AD∩ED=D,∴BE⊥平面ADE
∵BE?平面EAB,∴平面EAB⊥平面ADE,故(4)正确;
(5)∵BE⊥平面ADE,∴∠BAE为直线BA与平面ADE所成角
在△BAE中,∠BEA=90°,BE=a,AB=
a,∴sin∠BEA=
=
,故(5)正确
故答案为:(1)(2)(4)(5)
 解:由题意,AD⊥平面BCDE,AD=a,AC=
解:由题意,AD⊥平面BCDE,AD=a,AC=| 2 |
(1)由于BC∥DE,∴∠ABC(或其补角)为AB与DE所成角
∵AB=
| 3 |
| 2 |
| 2 |
(2)VB-ACE的体积是
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 6 |
(3)∵CD∥BE,∴AB与CD不平行,故(3)不正确;
(4)∵AD⊥平面BCDE,BE?平面BCDE,∴AD⊥BE,∵BE⊥ED,AD∩ED=D,∴BE⊥平面ADE
∵BE?平面EAB,∴平面EAB⊥平面ADE,故(4)正确;
(5)∵BE⊥平面ADE,∴∠BAE为直线BA与平面ADE所成角
在△BAE中,∠BEA=90°,BE=a,AB=
| 3 |
| BE |
| AB |
| ||
| 3 |
故答案为:(1)(2)(4)(5)
点评:本题考查图形的翻折,考查空间线面位置关系,搞清翻折前后的变与不变是关键.

练习册系列答案
相关题目
 (2012•安庆二模)函数f(x)的图象如图所示,已知函数F(x)满足F′(x)=f(x),则F(x)的函数图象可能是( )
(2012•安庆二模)函数f(x)的图象如图所示,已知函数F(x)满足F′(x)=f(x),则F(x)的函数图象可能是( )