题目内容
已知函数
．
（1）设f（x）的定义域为A，求集合A；
（2）判断函数f（x）在（1，+∞）上单调性，并用定义加以证明．
．（1）设f（x）的定义域为A，求集合A；
（2）判断函数f（x）在（1，+∞）上单调性，并用定义加以证明．
解：（1）由x2﹣1≠0，得x≠1，所以，函数
的定义域为x∈R|x≠1
（2）函数
在（1，+∞）上单调递减．
证明：任取x1，x2∈（1，+∞），设x1＜x2，
则△x=x2﹣x1＞0，
∵x1＞1，x2＞1，∴x12﹣1＞0，x22﹣1＞0，x1+x2＞0．
又x1＜x2，所以x1﹣x2＜0，
故△y＜0．
因此，函数
在（1，+∞）上单调递减
的定义域为x∈R|x≠1（2）函数
在（1，+∞）上单调递减．证明：任取x1，x2∈（1，+∞），设x1＜x2，
则△x=x2﹣x1＞0，
∵x1＞1，x2＞1，∴x12﹣1＞0，x22﹣1＞0，x1+x2＞0．
又x1＜x2，所以x1﹣x2＜0，
故△y＜0．
因此，函数
在（1，+∞）上单调递减
练习册系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
．
在
上单调递增，求
的取值范围。
与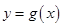
的图象有两个不同的交点M、N，求
轴的垂线分别与
的图像和
的图像交S、T点，以S为切点作
，以T为切点作
．是否存在实数
．
．
．
．