题目内容
已知函数
．（1）设f（x）的定义域为A，求集合A；
（2）判断函数f（x）在（1，+∞）上单调性，并用定义加以证明．
【答案】分析：（1）f（x）为分式函数，则由分母不能为零，解得定义域；
（2）要求用定义证明，则先在（1，+∞）上任取两变量且界定大小，然后作差变形看符号．
解答：解：（1）由x2-1≠0，得x≠±1，
所以，函数
的定义域为x∈R|x≠±1（4分）
（2）函数
在（1，+∞）上单调递减．（6分）
证明：任取x1，x2∈（1，+∞），设x1＜x2，
则△x=x2-x1＞0，
（8分）
∵x1＞1，x2＞1，∴x12-1＞0，x22-1＞0，x1+x2＞0．
又x1＜x2，所以x1-x2＜0，故△y＜0．
因此，函数
在（1，+∞）上单调递减．（12分）
点评：本题主要考查函数定义域的基本求法和单调性定义证明函数的单调性．
（2）要求用定义证明，则先在（1，+∞）上任取两变量且界定大小，然后作差变形看符号．
解答：解：（1）由x2-1≠0，得x≠±1，
所以，函数
的定义域为x∈R|x≠±1（4分）（2）函数
在（1，+∞）上单调递减．（6分）证明：任取x1，x2∈（1，+∞），设x1＜x2，
则△x=x2-x1＞0，
（8分）∵x1＞1，x2＞1，∴x12-1＞0，x22-1＞0，x1+x2＞0．
又x1＜x2，所以x1-x2＜0，故△y＜0．
因此，函数
在（1，+∞）上单调递减．（12分）点评：本题主要考查函数定义域的基本求法和单调性定义证明函数的单调性．
练习册系列答案
相关题目
．
在
上单调递增，求
的取值范围。
与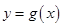
的图象有两个不同的交点M、N，求
轴的垂线分别与
的图像和
的图像交S、T点，以S为切点作
，以T为切点作
．是否存在实数
．
．
．