题目内容
已知f(x)=ax3+bx2+cx(a≠0)在x=±1处取得极值，且f(1)=-1.（1）求常数a、b、c的值；
（2）求f(x)的极值.
解:（1）f′(x)=3ax2+2bx+c,由已知有
f′(1)=f′(-1)=0,f(1)=-1,
即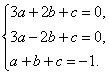
解得a=
，b=0，c=-
.
（2）由（1）,知f(x)=
x3-
x,
∴f′(x)= 
x2-
=
(x-1)(x＋1).
当x＜-1或x＞1时，f′(x)＞0,当-1＜x＜1时,f′(x)＜0.
∴f(x)在(-∞,-1)和(1,+∞)内都为增函数,在（-1，1）内是减函数.
因此，当x=-1时，函数f(x)取得极大值f(-1)=1；当x=1时，
函数f(x)取得极小值f(1)=-1.
练习册系列答案
相关题目
已知f(x)=ax3+ln(
+x)+2，且f（-5）=m，则f（5）+f（-5）的值为（ ）
| x2+1 |
| A、4 | B、0 | C、2m | D、-m+4 |
已知f(x)=ax3+
(ab≠0)，对任意a，b∈R（a≠b），都有
＞0．若x1+x2＜0，且x1?x2＜0，则f（x1）+f（x2）的值（ ）
| b |
| x |
| f(a)-f(b) |
| a-b |
| A、恒小于0 | B、恒大于0 |
| C、可能为0 | D、可正可负 |