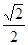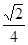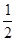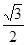题目内容
直线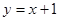 被椭圆
被椭圆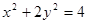 所截得的弦的中点坐标是( )
所截得的弦的中点坐标是( )
A.(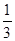 , , 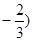 | B.(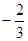 , , 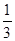 ) ) | C.(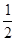 , ,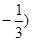 | D.(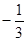 , , 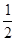 ) ) |
B
解析试题分析:由 ,得:
,得: 即
即
设弦 的两端点的坐标分别为:
的两端点的坐标分别为: ,
,
所以

所以弦 的中点的坐标为
的中点的坐标为 ,即
,即
考点:本小题主要考查直线与椭圆相交时弦的中点问题,考查学生的运算能力.
点评:遇到直线与椭圆相交问题,一般免不了要联立方程组,运算量比较大,学生要仔细、准确的计算.

练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案
相关题目
动点 到点
到点 及点
及点 的距离之差为2,则点
的距离之差为2,则点 的轨迹是
的轨迹是
| A.双曲线 | B.双曲线的一支 | C.两条射线 | D.一条射线 |
双曲线 的渐近线方程是( )
的渐近线方程是( )
A. | B. | C. | D. |
椭圆 上一点
上一点 到焦点
到焦点 的距离为2,
的距离为2, 是
是 的中点,则
的中点,则 等于( )
等于( )
| A.2 | B. | C. | D. |
设椭圆 的右焦点与抛物线
的右焦点与抛物线 的焦点相同,离心率为
的焦点相同,离心率为 ,则此椭圆的方程为( )
,则此椭圆的方程为( )
A. | B. | C. | D. |
已知点 在抛物线
在抛物线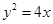 上,则点
上,则点 到直线
到直线 的距离和到直线
的距离和到直线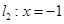 的距离之和的最小值为( )
的距离之和的最小值为( )
A.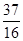 | B.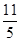 | C.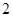 | D.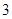 |
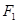 和
和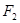 分别是双曲线
分别是双曲线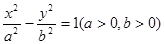 的两个焦点,
的两个焦点, 和
和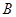 是以
是以 为圆心,以
为圆心,以 为半径的圆与该双曲线左支的两个交点,且△
为半径的圆与该双曲线左支的两个交点,且△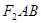 是等边三角形,则双曲线的离心率为( )
是等边三角形,则双曲线的离心率为( )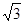
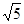
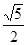
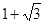
 的右顶点为
的右顶点为 ,
, 分别交于
分别交于 两点,其中
两点,其中 为坐标原点,则
为坐标原点,则 与
与 的大小关系为( )
的大小关系为( )


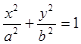 (a>b>0)的左焦点, P是椭圆上的一点, PF⊥x轴, O
(a>b>0)的左焦点, P是椭圆上的一点, PF⊥x轴, O