题目内容
已知非零向量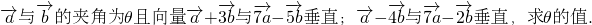
解：∵
与
垂直，
∴
=0，
∴
=0，①
∵
与
垂直，
∴
=0 ②
②-①得
③
把③代入②得，
，
∴cosθ=
=
，
∵θ∈[0，π]
∴
分析：根据所给的两组向量垂直，得到两组向量的数量积为0，把两个式子进行比较得到等量关系，在求两个向量夹角的时候，把所得的等量关系代入公式，约分化简，得到余弦值，从而得到角．
点评：本题考查数量积的应用，数量积的主要应用：①求模长；②求夹角；③判垂直，本题是应用中的求夹角，解题过程中注意夹角本身的范围，避免出错．
与垂直，∴
=0，∴
=0，①∵
与垂直，∴
=0 ②②-①得
③把③代入②得，
，∴cosθ=
=，∵θ∈[0，π]
∴
分析：根据所给的两组向量垂直，得到两组向量的数量积为0，把两个式子进行比较得到等量关系，在求两个向量夹角的时候，把所得的等量关系代入公式，约分化简，得到余弦值，从而得到角．
点评：本题考查数量积的应用，数量积的主要应用：①求模长；②求夹角；③判垂直，本题是应用中的求夹角，解题过程中注意夹角本身的范围，避免出错．
练习册系列答案
相关题目
已知非零向量
，
，若2
+3
与2
-3
互相垂直，则|
|=（ ）
| a |
| b |
| a |
| b |
| a |
| b |
| ||
|
A、
| ||
B、
| ||
C、
| ||
D、
|
已知非零向量
，
，
满足
+
+
=0，且
与
的夹角为60°，|
|=
|
|，则
与
的夹角为（ ）
| a |
| b |
| c |
| a |
| b |
| c |
| a |
| c |
| b |
| 3 |
| a |
| a |
| b |
| A、30° | B、150° |
| C、60° | D、120° |
给定命题p：若x2≥0，则x≥0；命题q：已知非零向量
，
，则“
⊥
”是“|
-
|=|
+
|”的充要条件．则下列各命题中，假命题的是（ ）
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| A、p∨q |
| B、（?p）∨q |
| C、（?p）∧q |
| D、（?p）∧（?q） |