题目内容
设函数f(x)=x3-6x2+2,x∈R(1)求f(x)的极值;
(2)当x∈[-a,a]时,求f(x)的最大值;
(3)设g(x)=|f(x)-k|,x∈(0,6),用φ(k)表示g(x)的最大值,求φ(k)的解析式和φ(k)的最小值及相应的k的值.
解:(1)f(x)=x3-6x2+2,![]() (x)=3x2-12x=3x(x-4) 令
(x)=3x2-12x=3x(x-4) 令![]() (x)=0得x1=0,x2=4.
(x)=0得x1=0,x2=4.
列表如下
x | (-∞,0) | 0 | (0,4) | 4 | (4,+∞) |
| + | 0 | - | 0 | + |
f(x) | ↗ | 极大值2 | ↘ | 极小值-30 | ↗ |
从而当x=0时,f(x)取得极大值2;
当x=4时,f(x)取得极小值-30
(2)根据(1)可知f(0)=2是极大值,在(4,+∞)内函数f(x)单调递增,并且可验证f(6)=2,由条件知a>0因此在[-a,a]上,当0<a≤6时,f(x)的最大值与极大值f(0)=2相同
当a>6时,f(x)的最大值是f(a)=a3-6a2+2.
即f(x)max=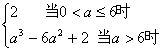
(3)f(x)-k=x3-6x2+2-k,
∴![]() =3x(x-4).
=3x(x-4).
令![]() =0得x1=0 x2=4.
=0得x1=0 x2=4.
又由于f(0)-k=f(6)-k=2-k,f(4)-k=-30-k,所以当x∈[0,6]时,g(x)=|f(x)-k|的最大值φ(k)=max{|2-k|,
|30+k|}.
当k变化时|2-k|和|30+k|的图像如图a所示
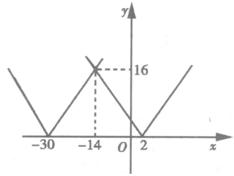
图a
从而φ(k)的图像如图b
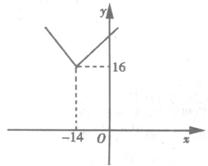
图b
因此φ(k)=![]()
并且当k=-14时,φ(x)取得最小值16.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
设函数f(x)=x3-(
)x-2,则其零点所在区间为( )
| 1 |
| 2 |
| A、(0,1) |
| B、(1,2) |
| C、(2,3) |
| D、(3,4) |