题目内容
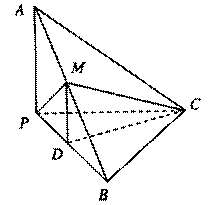
如图,三棱锥A—BPC中,AP⊥PC,AC⊥BC,M为AB中点,D为PB中点,且△PMB为正三角形.
(Ⅰ)求证:DM//平面APC;
(Ⅱ)求 证:平面ABC⊥平面APC;
|
解:(Ⅰ)∵M为AB中点,D为PB中点,
∴MD//AP, 又∴MD![]() 平面ABC
平面ABC
∴DM//平面APC ……………3分
(Ⅱ)∵△PMB为正三角形,且D为PB中点。
∴MD⊥PB
又由(Ⅰ)∴知MD//AP, ∴AP⊥PB
又已知AP⊥PC ∴AP⊥平面PBC,
∴AP⊥BC, 又∵AC⊥BC
∴BC⊥平面APC, ∴平面ABC⊥平面PAC ……………8分
(Ⅲ)∵AB=20![]()
∴MB=10 ∴PB=10
又BC=4,![]()
∴![]()
又MD![]()
∴VD-BCM=![]() VM-BCD=
VM-BCD=![]() ………………12分
………………12分

练习册系列答案
相关题目
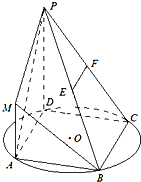 在如图所示的几何体中,平行四边形ABCD的顶点都在以AC为直径的圆O上,AD=CD=DP=a,AP=CP=
在如图所示的几何体中,平行四边形ABCD的顶点都在以AC为直径的圆O上,AD=CD=DP=a,AP=CP= 在如图所示的几何体中,平行四边形ABCD的顶点都在以AC为直径的圆O上,AD=CD=DP=a,AP=CP=
在如图所示的几何体中,平行四边形ABCD的顶点都在以AC为直径的圆O上,AD=CD=DP=a,AP=CP= a,DP∥AM,且AM=
a,DP∥AM,且AM= DP,E,F分别为BP,CP的中点.
DP,E,F分别为BP,CP的中点.


