题目内容
如图,在三棱锥P-ABC中,AC=BC=2,∠ACB=90°,AP=BP=AB,PC⊥AC.

(Ⅰ)求证:PC⊥A![]() ;
;
(Ⅱ)求二面角B-AP-C的大小;
(Ⅲ)求点C到平面APB的距离.
解法一:
(1)取AB中点D,连结PD,CD.

∵AP=BP,∴PD⊥AB.
∵AC=BC,∴CD⊥AB.
∵PD∩CD=D,∴AB⊥平面PCD.
∵PC∩平面PCD.
∴PC⊥AB.
(Ⅱ)∵AC=BC,AP=BP,∴△APC≌△BPC.
又PC⊥BC. ∴PC⊥BC.
又∠ACB=90°,即AC⊥BC.
且AC∩PC=C,
∴BC⊥平面PAC.
取AP中点E,连结BE,CE.

∵AB=BP,∴BE⊥AP.
∵EC是BE在平面PAC内的射影,∴CE⊥AP.
∴∠BEC是二面角B-AP-C的平面角.
在△BCE中,∠BCE=90°,BC=2,BE=![]() AB=
AB=![]() ,
,
∴sin∠BEC=![]()
∴二面角B-AP-C的大小为 arcsin![]()
(Ⅲ)由(Ⅰ)知AB⊥平面PCD,
∴平面APB⊥平面PCD.
过C作CH⊥PD,垂足为H.

∵平面APB∩平面PCD=PD,
∴CH⊥平面APB.
∴CH的长即为点C到平面APB的距离,
由(Ⅰ)知PC⊥AB,又PC⊥AC,
且AB∩AC=A.
∴PC⊥平面ABC.
CD![]() 平面ABC.
平面ABC.
∴PC⊥CD.
在Rt△PCD中,CD=![]()
∴PC=![]()
∴CH=![]()
∴点C到平面APB的距离为![]()
解法二:
(Ⅰ)∵AC=BC,AP=BP,
∴△APC≌△BPC.
又PC⊥AC.
∴PC⊥BC.
∵AC∩BC=C,
∴PC⊥平面ABC.
∵AB![]() 平面ABC,
平面ABC,
∴PC⊥AB.
(Ⅱ)如图,以C为原点建立空间直角坐标系C-xyz.,则C(0,0,0),A(0,2,0),B(2,0,0).设P(0,0,1).

∵|PB|=|AB|=2![]() ,
,
∴t=2,P(0,0,2).
取AP中点E,连结BE,CE.
∵|AC|=|PC|,|AB|=|BP|,
∴CE⊥AP,BE⊥AP.
∴∠BEC是二面角B-AP-C的平面角.
∵E(0,1,1),![]()
∴cos∠BEC=
∴二面角B-AP-C的大小为arccos![]()
(Ⅲ)∵AC=BC=PC,
∴C在平面APB内的射影为正△APB的中心H,且CH的长为点C到平面APB的距离.
如(Ⅱ)建立空间直角坐标系C-xyZ.
∵![]()
∴点H的坐标为(![]() ).
).
∴![]()
∴点C到平面APB的距离为![]()

 快乐5加2金卷系列答案
快乐5加2金卷系列答案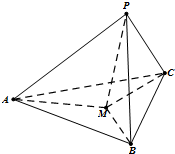 如图,在三棱锥P-ABC中,PA、PB、PC两两垂直,且PA=3.PB=2,PC=1.设M是底面ABC内一点,定义f(M)=(m,n,p),其中m、n、p分别是三棱锥M-PAB、三棱锥M-PBC、三棱锥M-PCA的体积.若f(M)=(
如图,在三棱锥P-ABC中,PA、PB、PC两两垂直,且PA=3.PB=2,PC=1.设M是底面ABC内一点,定义f(M)=(m,n,p),其中m、n、p分别是三棱锥M-PAB、三棱锥M-PBC、三棱锥M-PCA的体积.若f(M)=( 如图,在三棱锥P-ABC中,PA⊥底面ABC,∠ACB=90°,AE⊥PB于E,AF⊥PC于F,若PA=AB=2,∠BPC=θ,则当△AEF的面积最大时,tanθ的值为( )
如图,在三棱锥P-ABC中,PA⊥底面ABC,∠ACB=90°,AE⊥PB于E,AF⊥PC于F,若PA=AB=2,∠BPC=θ,则当△AEF的面积最大时,tanθ的值为( ) 如图,在三棱锥P-ABC中,PA=PB=AB=2,BC=3,∠ABC=90°,平面PAB⊥平面ABC,D、E分别为AB、AC中点.
如图,在三棱锥P-ABC中,PA=PB=AB=2,BC=3,∠ABC=90°,平面PAB⊥平面ABC,D、E分别为AB、AC中点. 如图,在三棱锥P-ABC中,已知PA=PB=PC,∠BPA=∠BPC=∠CPA=40°,一绳子从A点绕三棱锥侧面一圈回到点A的最短距离是
如图,在三棱锥P-ABC中,已知PA=PB=PC,∠BPA=∠BPC=∠CPA=40°,一绳子从A点绕三棱锥侧面一圈回到点A的最短距离是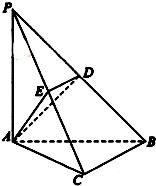 如图,在三棱锥P-ABC中,PA⊥底面ABC,∠BCA=90°,AP=AC,点D,E分别在棱
如图,在三棱锥P-ABC中,PA⊥底面ABC,∠BCA=90°,AP=AC,点D,E分别在棱