题目内容
M为△ABC的重心，
=（3，1），
=（4，-1）则
=
| AB |
| AC |
| AM |
(
，0)
| 7 |
| 3 |
(
，0)
．| 7 |
| 3 |
分析：本题可以作出辅助线取AC中点E，连接DE，利用中位线性质，三角形相似，得出AG=
AD，再利用向量共线定理
=
来解答．
| 2 |
| 3 |
| AG |
| 2 |
| 3 |
| AD |
解答：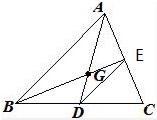
证明：如图取AC中点E，连接DE，则DE∥AB，且DE=
AB，
易得△GDE∽△GAE，所以DG=
AG，从而AG=
AD
由向量加法的平行四边形法则得：
=
(
+
)，
与
共线，
所以
=
，
即：
=
•
(
+
)=
(
+
)
∵
=（3，1），
=（4，-1），
则
=
[（3，1）+（4，-1）]=(
，0)．
故答案为：(
，0)．
证明：如图取AC中点E，连接DE，则DE∥AB，且DE=| 1 |
| 2 |
易得△GDE∽△GAE，所以DG=
| 1 |
| 2 |
| 2 |
| 3 |
由向量加法的平行四边形法则得：
| AD |
| 1 |
| 2 |
| AB |
| AC |
| AG |
| AD |
所以
| AG |
| 2 |
| 3 |
| AD |
即：
| AG |
| 2 |
| 3 |
| 1 |
| 2 |
| AB |
| AC |
| 1 |
| 3 |
| AB |
| AC |
∵
| AB |
| AC |
则
| AM |
| 1 |
| 3 |
| 7 |
| 3 |
故答案为：(
| 7 |
| 3 |
点评：本题考查向量加法及三角形，平行四边形法则，共线向量定理和平面向量基本定理的应用，利用向量基底表示平面内向量的方法．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
+
+
=
设a，b，c分别为△ABC的内角A，B，C的对边，点M为△ABC的重心．如a
+b
+
c
=
，则内角A的大小为 ；若a=3，则△ABC的面积为 ．