题目内容
已知数列的通项公式an=2n-37，当n等于多少时，Sn取最小值？并求此时Sn值．
分析：先令2n-37≥0求得数列从地19项开始为正数，前18项为负，推断出数列的前n项的和中，前18项的和最小，进而利用等差数列的求和公式求得答案．
解答：解：令2n-37≥0求得n＞18
即数列从地19项开始为正数，前18项为负，
故数列的前18项的和最小，
a18=-1，a1=-35
∴S18=
=-324
当n等于18时，Sn取最小值，此时Sn=-324．
即数列从地19项开始为正数，前18项为负，
故数列的前18项的和最小，
a18=-1，a1=-35
∴S18=
| (-35-1)×18 |
| 2 |
当n等于18时，Sn取最小值，此时Sn=-324．
点评：本题主要考查了等差数列的性质，求和公式以及数列与不等式的综合．解题的关键是分析出数列的正数项或负数项．
练习册系列答案
相关题目
已知数列的通项公式an=
(n∈N*)，则数列{an}的前30项中最大值和最小值分别是（ ）
n-
| ||
n-
|
| A、a10，a9 |
| B、a10，a30 |
| C、a1，a30 |
| D、a1，a9 |
已知数列
的通项公式
,设其前n项和为
，则使
成立的自然
数
有 （ ）
| A．最大值15 | B．最小值15 | C．最大值16 | D．最小值16 |
的通项公式为
，设其前
项和为
，则使
成立的最小自然数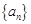
的通项公式为
，则数列
成等比数列是数列
的通项公式为
的( ▲ )