题目内容
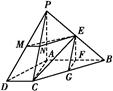
如图所示,正方形ADEF与梯形ABCD所在的平面互相垂直,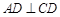 ,
,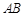 ∥
∥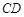 ,
, .
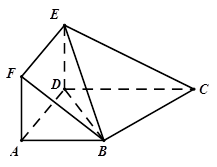
.
(1)求证: ;
;
(2)求直线 与平面
与平面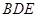 所成角的正切值;
所成角的正切值;
(3)在 上找一点
上找一点 ,使得
,使得 ∥平面ADEF,请确定M点的位置,并给出证明.
∥平面ADEF,请确定M点的位置,并给出证明.
(1)见解析;(2) .(3)M是EC中点,BM∥面ADEF.
.(3)M是EC中点,BM∥面ADEF.
解析试题分析:(1)由已知:面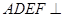 面
面 ,
, ,得到
,得到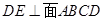 ,
,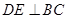 .
.
取 四边形
四边形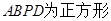 .
.
由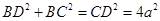 ,得到
,得到 ,
,
根据 证得
证得 .
.
(2)由(1)可知:
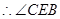 即为CE与面BDE所成的角.
即为CE与面BDE所成的角.
在 中,可得
中,可得 .
.
(3)取EC中点M,则BM∥面ADEF,证明思路如下:
连结MB、MP,由(1)知BP∥AD,得到BP∥面ADEF,在 由三角形中位线定理,可得
由三角形中位线定理,可得 ∥
∥ ,进一步可得证.
,进一步可得证.
试题解析:(1)由已知:面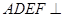 面
面 ,面
,面 面
面
 .
. ,
, ,
,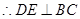 .
.
取
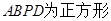 .
.
设
 ,
, ,
,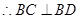 ,
,
从而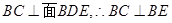 . 4分
. 4分
(2)由(1)可知:
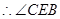 即为CE与面BDE所成的角.
即为CE与面BDE所成的角. 中,
中, ,
,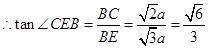 . 8分
. 8分
(3)取EC中点M,则BM∥面ADEF,证明如下:
连结MB、MP,由(1)知BP∥AD,∴BP∥面ADEF, M、P分别为EC、DC的中点,
M、P分别为EC、DC的中点, ∥
∥ ,∴MP∥面ADEF,∴面BMP∥面ADEF,∴BM∥面ADEF. 12分
,∴MP∥面ADEF,∴面BMP∥面ADEF,∴BM∥面ADEF. 12分
考点:平行关系,垂直关系,线面角的计算.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 中,已知
中,已知 的直径
的直径 的中点.
的中点.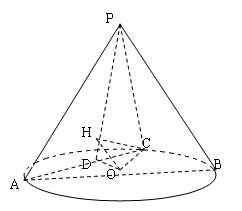
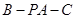 的余弦值.
的余弦值. 为正方形,四边形
为正方形,四边形 是直角梯形,
是直角梯形, ,
, 平面
平面 .
.
 平面
平面 ;
; 与平面
与平面
 AB.Q是PC上的一点.
AB.Q是PC上的一点.
 中,侧面
中,侧面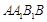 为菱形,且
为菱形,且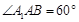 ,
, ,
,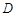 是
是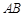 的中点.
的中点.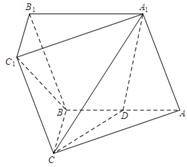
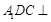 平面
平面 ;
; ∥平面
∥平面 .
. 的底面是边长为2的正三角形,且侧棱垂直于底面,侧棱长是,D是AC的中点。
的底面是边长为2的正三角形,且侧棱垂直于底面,侧棱长是,D是AC的中点。
 平面
平面 ;
; 的大小;
的大小; 与平面
与平面 ABCD中,AB⊥AC,AB⊥PA,AB∥CD,AB=2CD,E,F,G,M,N分别为PB,AB,BC,PD,PC的中点
ABCD中,AB⊥AC,AB⊥PA,AB∥CD,AB=2CD,E,F,G,M,N分别为PB,AB,BC,PD,PC的中点