题目内容
如图，已知P是正方形ABCD平面外一点,M,N分别是PA,BD上的点,且PM∶MA=BN∶ND=5∶8,求证:直线MN∥平面PBC.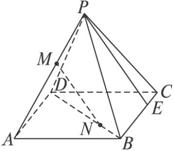
分析：欲证直线MN∥平面PBC,只需证明
与平面PBC内的某一向量a共线即可,即
=λa,λ∈R.
证明：
.
在BC上取点E，使BE=
BC，
于是
=
（
）=
.
所以MN∥PE.所以MN∥平面PBC.
点拨：用向量知识解题,一般不需要作辅助线,只是利用向量运算及基本定理,把要证的向量用该平面内的向量表示.
练习册系列答案
金钥匙试卷系列答案
相关题目
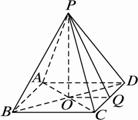
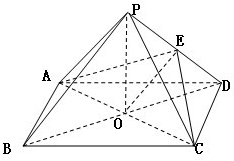如图：已知P是正方形ABCD所在平面外一点，点P在平面ABCD内的射影O是正方形的中心，PO=OD=a，E是PD的中点
= 
+x
+y
；??
=x
+y
+
.?
