题目内容
对于问题:“已知关于x的不等式ax2+bx+c>0的解集为(-1,2),解关于x的不等式ax2-bx+c>0”,给出如下一种解法:解:由ax2+bx+c>0的解集为(-1,2),得a(-x)2+b(-x)+c>0的解集为(-2,1),即关于x的不等式ax2-bx+c>0的解集为(-2,1).参考上述解法,若关于x的不等式| k |
| x+a |
| x+b |
| x+c |
| 1 |
| 3 |
| 1 |
| 2 |
| kx |
| ax+1 |
| bx+1 |
| cx+1 |
分析:观察发现ax2+bx+c>0将x换成-x得a(-x)2+b(-x)+c>0,则解集也相应变化,-x∈(-1,2),则x∈(-2,1)
不等式
+
<0将x换成
得不等式
+
<0,故
∈(-1,-
)∪(
,1),分析可得答案.
不等式
| k |
| x+a |
| x+b |
| x+c |
| 1 |
| x |
| kx |
| ax+1 |
| bx+1 |
| cx+1 |
| 1 |
| x |
| 1 |
| 3 |
| 1 |
| 2 |
解答:解:由ax2+bx+c>0的解集为(-1,2),得a(-x)2+b(-x)+c>0的解集为(-2,1),
发现-x∈(-1,2),则x∈(-2,1)
若关于x的不等式
+
<0的解集为(-1,-
)∪(
,1),
则关于x的不等式
+
<0可看成前者不等式中的x用
代入可得,
则
∈(-1,-
)∪(
,1),则x∈(-3,-1)∪(1,2),
故答案为(-3,-1)∪(1,2).
发现-x∈(-1,2),则x∈(-2,1)
若关于x的不等式
| k |
| x+a |
| x+b |
| x+c |
| 1 |
| 3 |
| 1 |
| 2 |
则关于x的不等式
| kx |
| ax+1 |
| bx+1 |
| cx+1 |
| 1 |
| x |
则
| 1 |
| x |
| 1 |
| 3 |
| 1 |
| 2 |
故答案为(-3,-1)∪(1,2).
点评:本题考查了类比推理,通过已知条件发现规律,属于基础题.

练习册系列答案
相关题目

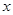 的不等式
的不等式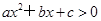 的解集为
的解集为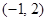 ,解关于
,解关于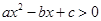 ”,给出如下一种解法:
”,给出如下一种解法: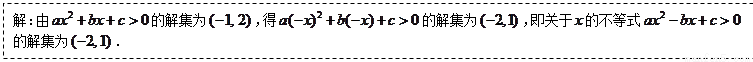 参考上述解法,若关于
参考上述解法,若关于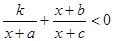 的解集为
的解集为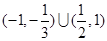 ,则关于
,则关于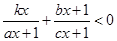 的解集为 。
的解集为 。 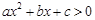 的解集为(-1,2),解关于x的不等式
的解集为(-1,2),解关于x的不等式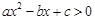 ”,给出如下一种解法:
”,给出如下一种解法: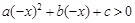 的解为
的解为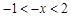 ,即关于x的不等式
,即关于x的不等式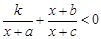 的解集为
的解集为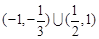 ,则关于x的不等式
,则关于x的不等式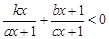 的解集为
※ .
的解集为
※ . 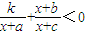 的解集为
的解集为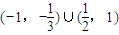 ,则关于x的不等式
,则关于x的不等式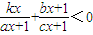 的解集为 .
的解集为 .