题目内容
【题目】如图,AB是⊙O的直径,C是⊙O上一点,∠ACD=∠B,AD⊥CD.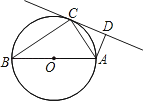
(1)求证:CD是⊙O的切线;
(2)若AD=1,OA=2,求AC的值.
【答案】
(1)
证明:连接OC,如图所示:

∵AB是⊙O直径,
∴∠ACB=90°,
∵OB=OC,
∴∠B=∠BCO,
又∵∠ACD=∠B,
∴∠OCD=∠OCA+∠ACD=∠OCA+∠BCO=∠ACB=90°,
即OC⊥CD,
∴CD是⊙O的切线;
(2)
解:∵AD⊥CD,
∴∠ADC=∠ACB=90°,
又∵∠ACD=∠B,
∴△ACB∽△ADC,
∴AC2=ADAB=1×4=4,
∴AC=2.
【解析】本题考查了切线的判定、等腰三角形的性质、相似三角形的判定与性质;熟练掌握切线的判定,证明三角形相似是解决问题(2)的关键.(1)连接OC,由圆周角定理得出∠ACB=90°,由等腰三角形的性质得出∠B=∠BCO,证出∠OCD=∠OCA+∠BCO=∠ACB=90°,即可得出结论;(2)证明△ACB∽△ADC,得出AC2=ADAB,即可得出结果.
【考点精析】掌握切线的判定定理是解答本题的根本,需要知道切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线.

【题目】在生产过程中,测得纤维产品的纤度(表示纤维粗细的一种量)共有100个数据,将数据分组如表:
分组 | 频数 |
|
|
|
|
|
|
|
|
|
|
|
|
合计 |
|
(1)画出频率分布表,并画出频率分布直方图;
(2)估计纤度落在![]() 中的概率及纤度小于
中的概率及纤度小于![]() 的概率是多少?
的概率是多少?
(3)从频率分布直方图估计出纤度的众数、中位数和平均数.
【题目】为了让学生更多的了解“数学史”知识,梁才学校高二年级举办了一次“追寻先哲的足迹,倾听数学的声音”的数学史知识竞赛活动,共有800名学生参加了这次竞赛.为了解本次竞赛的成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计,统计结果见下表.请你根据频率分布表解答下列问题:
序号 | 分组 | 组中值 | 频数 | 频率 |
(i) | (分数) | (Gi) | (人数) | (Fi) |
1 |
| 65 | ① | 0.12 |
2 |
| 75 | 20 | ② |
3 |
| 85 | ③ | 0.24 |
4 |
| 95 | ④ | ⑤ |
合计 | 50 | 1 | ||
(1)填充频率分布表中的空格;
(2)为鼓励更多的学生了解“数学史”知识,成绩不低于85分的同学能获奖,请估计在
参加的800名学生中大概有多少名学生获奖?(3)在上述统计数据的分析中有一项计算见算法流程图,求输出的S的值.