题目内容
直线l1过点(﹣2,0)且倾斜角为30°,直线l2过点(2,0)且与直线l1垂直,则直线l1与直线l2的交点坐标为 .
考点:
两条直线的交点坐标.
专题:
直线与圆.
分析:
用点斜式求出两条直线的方程,再联立方程组,解方程组求得直线l1与直线l2的交点坐标.
解答:
解:由题意可得直线l1的斜率等于tan30°=![]() ,由点斜式求得它的方程为 y﹣0=
,由点斜式求得它的方程为 y﹣0=![]() (x+2),
(x+2),
即 ![]() x﹣3y+2
x﹣3y+2![]() =0.
=0.
直线l2过的斜率等于 ![]() =﹣
=﹣![]() ,由点斜式求得它的方程为 y﹣0=﹣
,由点斜式求得它的方程为 y﹣0=﹣![]() (x﹣2),
(x﹣2),
即 ![]() x+y﹣2
x+y﹣2![]() =0.
=0.
由 ![]() ,解得
,解得 ![]() ,故直线l1与直线l2的交点坐标为
,故直线l1与直线l2的交点坐标为 ![]() ,
,
故答案为 ![]() .
.
点评:
本题主要考查用点斜式求直线的方程,两条直线垂直的性质,求两条直线的交点坐标,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
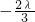 ,直线l1与l2相交于点P,其中λ∈R,
,直线l1与l2相交于点P,其中λ∈R,