题目内容
若1∈{a+2，（a+1）2，a2+3a+3}，则实数a=
0
0
．分析：由元素与集合的关系，本集合中三个元素都可能是1，故分类研究，求出参数的值再验证所得的结果是否能保证集合有意义，能保证有意义的即是可取值
解答：解：由题意，若a+2=1，得a=-1，代入得 {1，0，1}，无意义；
若（a+1）2=1，可得a=-2，或a=0，若a=0时，集合为{2，1，3} 有意义，若a=-2时，集合为{1，0，1}无意义，故a=0可取；
若a2+3a+3=1，可得a=-1，或a=-2，此两数都不能合集合有意义
综上，实数a的值为0
故答案为：0．
若（a+1）2=1，可得a=-2，或a=0，若a=0时，集合为{2，1，3} 有意义，若a=-2时，集合为{1，0，1}无意义，故a=0可取；
若a2+3a+3=1，可得a=-1，或a=-2，此两数都不能合集合有意义
综上，实数a的值为0
故答案为：0．
点评：本题考查元素与集合关系的判断，求解的关键是理解集合中三个元素都可能是1，要分三类来求解，以及求出参数后的验证，求解此类题易因为没有验证而多出两个解导致解题失败．
练习册系列答案
春雨教育同步作文系列答案
相关题目
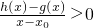在D内恒成立，则称P为函数y=h（x）的“类对称点”，请你探究当a=4时，函数y=f（x）是否存在“类对称点”，若存在，请最少求出一个“类对称点”的横坐标；若不存在，说明理由．
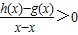在D内恒成立，则称P为函数y=h（x）的“类对称点”，请你探究当a=4时，函数y=f（x）是否存在“类对称点”，若存在，请最少求出一个“类对称点”的横坐标；若不存在，说明理由．
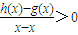在D内恒成立，则称P为函数y=h（x）的“类对称点”，请你探究当a=4时，函数y=f（x）是否存在“类对称点”，若存在，请最少求出一个“类对称点”的横坐标；若不存在，说明理由．