题目内容
在锐角△ABC中,三个内角A,B,C所对的边分别为a,b,c,若acsinC=(a2+c2-b2)sinB,
(1)若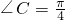 ,求∠A的大小.
,求∠A的大小.
(2)若三角形为非等腰三角形,求 的取值范围.
的取值范围.
解:(1)∵acsinC=(a2+c2-b2)sinB
∴ …(2分)
…(2分)
由此可得,sinC=2sinBcosB=sin2B…(3分)
因此,C=2B或C+2B=π…(4分)
(i)若C=2B,结合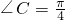 ,可得
,可得 ,所以
,所以 …(5分)
…(5分)
(ii)若C+2B=π,结合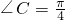 ,则
,则 ,可得
,可得 …(6分)
…(6分)
(2)∵三角形为非等腰三角形,
∴可得C+2B=π不能成立,故C=2B
由此可得∠A=π-B-C=π-3B…(8分)
又∵三角形为锐角三角形,∴
因此,可得 …(10分)
…(10分)
而 …(12分)
…(12分)
∵cosB∈( ,
, ),∴可得
),∴可得 =
= …(14分)
…(14分)
分析:(1)将已知等式变形,整理得 ,可得sinC=2sinBcosB=sin2B,由此可得C=2B或C+2B=π,最后结合三角形内角和定理和
,可得sinC=2sinBcosB=sin2B,由此可得C=2B或C+2B=π,最后结合三角形内角和定理和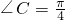 ,即可算出∠A的大小.
,即可算出∠A的大小.
(2)根据三角形为非等腰三角形,结合(1)中化简的结果可得C=2B,从而将 化简整理得
化简整理得 .利用△ABC是锐角三角形,得到B∈(
.利用△ABC是锐角三角形,得到B∈( ),结合余弦函数的图象与性质,即可得出
),结合余弦函数的图象与性质,即可得出 的取值范围.
的取值范围.
点评:本题给出三角形中的边角关系,要求我们判断角A的大小并求 的取值范围.着重考查了利用正余弦定理解三角形、三角形内角和定理与余弦函数的图象与性质等知识,属于中档题.
的取值范围.着重考查了利用正余弦定理解三角形、三角形内角和定理与余弦函数的图象与性质等知识,属于中档题.
∴
 …(2分)
…(2分)由此可得,sinC=2sinBcosB=sin2B…(3分)
因此,C=2B或C+2B=π…(4分)
(i)若C=2B,结合
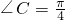 ,可得
,可得 ,所以
,所以 …(5分)
…(5分)(ii)若C+2B=π,结合
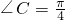 ,则
,则 ,可得
,可得 …(6分)
…(6分)(2)∵三角形为非等腰三角形,
∴可得C+2B=π不能成立,故C=2B
由此可得∠A=π-B-C=π-3B…(8分)
又∵三角形为锐角三角形,∴

因此,可得
 …(10分)
…(10分)而
 …(12分)
…(12分)∵cosB∈(
 ,
, ),∴可得
),∴可得 =
= …(14分)
…(14分)分析:(1)将已知等式变形,整理得
 ,可得sinC=2sinBcosB=sin2B,由此可得C=2B或C+2B=π,最后结合三角形内角和定理和
,可得sinC=2sinBcosB=sin2B,由此可得C=2B或C+2B=π,最后结合三角形内角和定理和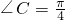 ,即可算出∠A的大小.
,即可算出∠A的大小.(2)根据三角形为非等腰三角形,结合(1)中化简的结果可得C=2B,从而将
 化简整理得
化简整理得 .利用△ABC是锐角三角形,得到B∈(
.利用△ABC是锐角三角形,得到B∈( ),结合余弦函数的图象与性质,即可得出
),结合余弦函数的图象与性质,即可得出 的取值范围.
的取值范围.点评:本题给出三角形中的边角关系,要求我们判断角A的大小并求
 的取值范围.着重考查了利用正余弦定理解三角形、三角形内角和定理与余弦函数的图象与性质等知识,属于中档题.
的取值范围.着重考查了利用正余弦定理解三角形、三角形内角和定理与余弦函数的图象与性质等知识,属于中档题. 
练习册系列答案
相关题目