题目内容
【题目】定义在
上的函数
，如果对任意
，恒有
成立，则称为
阶缩放函数．
（1）已知函数为二阶缩放函数，且当
时，
，求
的值；
（2）已知函数为二阶缩放函数，且当时，
，求证：函数
在
上无零点；
（3）已知函数为阶缩放函数，且当
时， 的取值范围是
，求在
上的取值范围．
【答案】（1）1；（2）证明见解析；（3）
【解析】
（1）根据二阶缩放函数的定义，直接代入进行求值即可；
（2）根据函数零点的定义和性质判断函数
在
上无零点；
（3）根据
阶缩放函数成立的条件建立条件关系即可求出结论．
（1）由
得，
，
（2）当
时，
，依题意可得：
．…
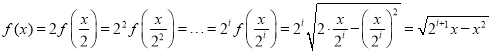方程
或
，0与
均不属于
当
时，方程
无实数解．
注意到
，
所以函数在上无零点．
（3）当
时，有
，
依题意可得：
当
时，
的取值范围是
…
所以当时， 的取值范围是
．…
由于
所以函数在
上的取值范围是：
练习册系列答案
轻松暑假总复习系列答案
相关题目
