题目内容
9.已知不等式x2<logax在x∈(0,$\frac{1}{2}$)时恒成立,则实数a的取值范围为( )| A. | (0,1) | B. | [$\frac{1}{16}$,1) | C. | (0,$\frac{1}{16}$) | D. | (1,+∞) |
分析 构造函数:设f(x)=x2,g(x)=logax,作出函数图象,利用数形结合得出$\left\{\begin{array}{l}0<a<1\\ f(\frac{1}{2})≤g(\frac{1}{2})\end{array}\right.$,解出a的范围即可.
解答 解:∵x2<logax.
设f(x)=x2,g(x)=logax.
∴当x∈(0,$\frac{1}{2}$)时,函数f(x)的图象在函数g(x)的图象的下方,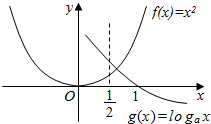
∴$\left\{\begin{array}{l}{0<a<1}\\{f(\frac{1}{2})≤g(\frac{1}{2})}\end{array}\right.$
即$\left\{\begin{array}{l}{0<a<1}\\{(\frac{1}{2})^{2}≤lo{g}_{a}\frac{1}{2}}\end{array}\right.$
∴$\frac{1}{16}$≤a<1.
故选:B.
点评 考查了利用数学结合思想做题,通过图象,直观的分析问题.数学结合是数学中的一种重要解题思想,应学会掌握.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
19.使对数loga(一2a+1)有意义的a的取值范围为( )
| A. | a>$\frac{1}{2}$且a≠1 | B. | 0<a<$\frac{1}{2}$ | C. | a>0且a≠1 | D. | a<$\frac{1}{2}$ |
4.设l是直线,α,β是两个不同的平面,则下列判断正确的是( )
| A. | 若l∥α,l∥β,则α∥β | B. | 若α⊥β,l∥α,则l⊥β | C. | 若α⊥β,l⊥α,则l⊥β | D. | 若l⊥α,l⊥β,则α∥β |
19.已知数列{an}满足a1=1,an+1=an+2n,则a10=( )
| A. | 1 024 | B. | 1 023 | C. | 2 048 | D. | 2 047 |
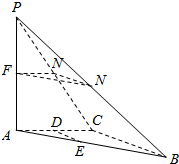 如图,在三棱锥P-ABC中,PA⊥平面ABC,AC⊥BC,D、E、F分别为AC、AB、AP的中点,M、N分别为线段PC、PB上的动点,且有MN⊥PC.
如图,在三棱锥P-ABC中,PA⊥平面ABC,AC⊥BC,D、E、F分别为AC、AB、AP的中点,M、N分别为线段PC、PB上的动点,且有MN⊥PC.