题目内容
已知函数 ;
;
(1)若 在
在 上单调递增,在
上单调递增,在 上单调递减,在
上单调递减,在 上单调递增,求实数
上单调递增,求实数 的值;
的值;
(2)当 时,求证:当
时,求证:当 时,
时,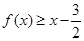 .
.
(1)  ;(2)分析法。
;(2)分析法。
解析试题分析:

 ,要证
,要证 ,即证
,即证 ,
,
令 ,
, 
 ,
, ,
,  在
在 ,
, 

考点:本题主要考查利用导数研究函数的单调性,利用导数证明不等式。
点评:中档题,本题属于导数应用中的基本问题,证明不等式,往往通过构造函数,确定函数的最值,达到证明目的。本题利用分析法,将问题做了进一步的转化,实现了化难为易。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 在x=
在x= 与x =l时都取得极值
与x =l时都取得极值 ,试比较
,试比较 与
与 的大小;
的大小; ,使得
,使得 对任意大于
对任意大于 的自然数
的自然数 都成立?若存在,试求出
都成立?若存在,试求出 的值并证明你的结论;若不存在,请说明理由。
的值并证明你的结论;若不存在,请说明理由。 ,
, .(其中
.(其中 为自然对数的底数).
为自然对数的底数).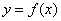 在
在 处的切线与直线
处的切线与直线 垂直,求
垂直,求 的值;
的值; ≥0,
≥0, 恒成立,试确定实数
恒成立,试确定实数 时,是否存在实数
时,是否存在实数 ,使曲线C:
,使曲线C: 在点
在点 处的切线与
处的切线与 轴垂直?若存在,求出
轴垂直?若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.  .
. 处的切线方程;
处的切线方程; ,若在[1,e]上至少存在一点
,若在[1,e]上至少存在一点 ,使得
,使得 成立,求实数p的取值范围.
成立,求实数p的取值范围.
 。
。 的最小值;
的最小值; 
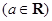 ,讨论函数
,讨论函数 的单调性;
的单调性; 的直线与曲线
的直线与曲线 交于
交于 ,
,
 两点,求证:
两点,求证: 。
。 ,
, 取得极值,求实数
取得极值,求实数 的值;
的值; 时,求
时,求 上的最小值;
上的最小值; ,直线
,直线 都不是曲线
都不是曲线 的切线,求实数
的切线,求实数 的图像在点
的图像在点 处的切线与直线
处的切线与直线 平行.
平行. 上恒成立,求a的取值范围;
上恒成立,求a的取值范围; (
( )
)