题目内容
若函数f(x)=sinωx+acosωx(ω>0)的图象关于点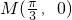 对称,且满足f(
对称,且满足f( )=f(
)=f(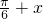 ),则a+ω的一个可能的取值是
),则a+ω的一个可能的取值是
- A.0
- B.1
- C.2
- D.3
D
分析:由题意可得,f(0)=f( ),可得关于a与ω的关系式;又f(
),可得关于a与ω的关系式;又f( )=f(
)=f(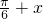 ),可知f(x)=sinωx+acosωx(ω>0)的图象关于直线x=
),可知f(x)=sinωx+acosωx(ω>0)的图象关于直线x= 对称,得关于a与ω的又一关系式;通过赋值可得答案.
对称,得关于a与ω的又一关系式;通过赋值可得答案.
解答:∵函数f(x)=sinωx+acosωx(ω>0)的图象关于点M( ,0)对称,
,0)对称,
∴f(0)=f( ),即a=sin
),即a=sin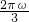 +acos
+acos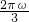 ,
,
又f( )=f(
)=f(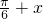 ),
),
∴f(x)=sinωx+acosωx(ω>0)的图象关于直线x= 对称,
对称,
∴f(0)=f( ),即a=sin
),即a=sin +acos
+acos ;
;
∴sin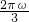 +acos
+acos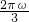 =sin
=sin +acos
+acos ;
;
不妨令ω=3,则0+a=0-a,
∴a=0,
∴a+ω=0+3.
即3是a+ω的一个可能值.
故选D.
点评:本题考查三角函数的性质,求得a是关键,考查正弦函数的对称性,考查分析、转化与运用三角知识解决问题的能力,属于难题.
分析:由题意可得,f(0)=f(
 ),可得关于a与ω的关系式;又f(
),可得关于a与ω的关系式;又f( )=f(
)=f(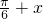 ),可知f(x)=sinωx+acosωx(ω>0)的图象关于直线x=
),可知f(x)=sinωx+acosωx(ω>0)的图象关于直线x= 对称,得关于a与ω的又一关系式;通过赋值可得答案.
对称,得关于a与ω的又一关系式;通过赋值可得答案.解答:∵函数f(x)=sinωx+acosωx(ω>0)的图象关于点M(
 ,0)对称,
,0)对称,∴f(0)=f(
 ),即a=sin
),即a=sin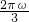 +acos
+acos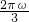 ,
,又f(
 )=f(
)=f(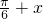 ),
),∴f(x)=sinωx+acosωx(ω>0)的图象关于直线x=
 对称,
对称,∴f(0)=f(
 ),即a=sin
),即a=sin +acos
+acos ;
;∴sin
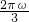 +acos
+acos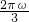 =sin
=sin +acos
+acos ;
;不妨令ω=3,则0+a=0-a,
∴a=0,
∴a+ω=0+3.
即3是a+ω的一个可能值.
故选D.
点评:本题考查三角函数的性质,求得a是关键,考查正弦函数的对称性,考查分析、转化与运用三角知识解决问题的能力,属于难题.

练习册系列答案
相关题目