题目内容
如图,在正方体ABCD—A1B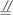
证明:∵E为D
∴A![]() EC1.
EC1.
∴四边形A1FC1E为平行四边形.
∴FC1∥A1E.
∴FC1∥平面A1BE.
∵F为A1B1的中点,H为B1B的中点,
∴FH∥A1B.
∴FH∥平面A1BE.
又FC1与FH相交于F,
∴平面FHC1∥平面A1BE.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
题目内容
如图,在正方体ABCD—A1B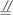
证明:∵E为D
∴A![]() EC1.
EC1.
∴四边形A1FC1E为平行四边形.
∴FC1∥A1E.
∴FC1∥平面A1BE.
∵F为A1B1的中点,H为B1B的中点,
∴FH∥A1B.
∴FH∥平面A1BE.
又FC1与FH相交于F,
∴平面FHC1∥平面A1BE.

 口算能手系列答案
口算能手系列答案