题目内容

a＞0,b＞0,a≠b,且a3-b3=a2-b2,求证:1＜a+b＜.

分析：从已知等式a3-b3=a2-b2a+b＞1是件容易的事,如何证a+b＜呢?用综合法难以下手,我们用分析法来证.

证明:∵a3-b3=a2-b2,

∴a2+ab+b2=a+b(∵a≠b).①

∴(a+b)2=a2+2ab+b2＞a2+ab+b2=(a+b).

∴a+b＞1.②

要证a+b＜,需证3(a+b)＜4,

于是证3(a+b)2＜4(a+b).

又由①式可知,必须证3(a2+b2+2ab)＜4(a2+ab+b2),

然后证a2-2ab+b2＞0,

即证(a-b)2＞0,而这一结论在a≠b时是恒成立的.

∴a+b＜.③

由②③知1＜a+b＜.

练习册系列答案
相关题目
（2009•虹口区一模）已知函数f（x）=ax2+bx+c（a，b，c为实数，a≠0），定义域D：[-1，1]
（1）当a=1，b=-1时，若函数f（x）在定义域内恒小于零，求c的取值范围；
（2）当a=1，常数b＜0时，若函数f（x）在定义域内恒不为零，求c的取值范围；
（3）当b＞2a＞0时，在D上是否存在x，使得|f（x）|＞b成立？（要求写出推理过程）
已知a＞0,b＞0,a+b=1,则+的取值范围是（    ）

A.(2,+∞)            B.［2,+∞)            C.(4,+∞)           D.［4,+∞)

若椭圆=1(m＞n＞0)和双曲线=1（a＞0,b＞0）有相同的焦点F1、F2，点P是两条曲线的一个交点，则|PF1|·|PF2|的值为（    ）

A.m-a          B.(m-a)             C.m2-a2             D.-

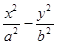设P是双曲线＝1(a＞0 ,b＞0)上的点，F1、F2是焦点，双曲线的离心 率是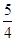，且∠F1PF2＝90°，△F1PF2面积是9，则a + b＝（   ）

A．4                B．5                C．6                D．7

 

若a＞0,b＞0,  a﹢b＝2,则下列不等式对一切满足条件的a,b 恒成立的是       

（写出所有正确命题的编号） 

①ab≤1    ②+≤   ③≥2    ④≥3  ⑤﹢≥2

 

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网