题目内容
4.已知向量$\overrightarrow{a}$=(-2,1),$\overrightarrow{b}$=(1,0),则|2$\overrightarrow{a}$+$\overrightarrow{b}$|=$\sqrt{13}$.分析 可进行向量坐标的加法和数乘运算求出向量$2\overrightarrow{a}+\overrightarrow{b}$的坐标,从而便可得出$|2\overrightarrow{a}+\overrightarrow{b}|$的值.
解答 解:$2\overrightarrow{a}+\overrightarrow{b}=(-3,2)$;
∴$|2\overrightarrow{a}+\overrightarrow{b}|=\sqrt{9+4}=\sqrt{13}$.
故答案为:$\sqrt{13}$.
点评 考查向量坐标的加法和数乘运算,以及根据向量的坐标求向量的长度.

练习册系列答案
相关题目
16.若a,b都是不等于1的正数,则“loga2>logb2”是“2a>2b”的( )
| A. | 充分非必要条件 | B. | 必要非充分条件 | ||
| C. | 充要条件 | D. | 非充分非必要条件 |
13.若复数z满足$\frac{z}{1-i}=i$,其中i为复数单位,则z=( )
| A. | 1-i | B. | 1+i | C. | -1-i | D. | -1+i |
14.秦九韶是我国古代数学家的杰出代表,他将一元n(n∈N*)次多项式的求值问题转化为n个一次式的算法叫秦九韶算法.如果没有秦九韶算法,人们在编程求axn(a≠0,1)值时需要设计n次乘法运算,现在利用秦九韶算法编程求f(x)=(n+1)xn+nxn-1+…+2x+1,当x=0.2的值时,所需乘法运算的次数比没有秦九韶算法所需乘法运算的次数少了( )
| A. | $\frac{{n}^{2}+n}{2}$ | B. | $\frac{{n}^{2}-n}{2}$ | C. | $\frac{{n}^{2}+n-2}{2}$ | D. | n |
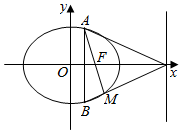 如图,已知椭圆C:$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1,F为该椭圆的右焦点,若AB为垂直于x轴的动弦,直线l:x=4与x轴交于点N,直线AF与BN交于点M(x0,y0).
如图,已知椭圆C:$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1,F为该椭圆的右焦点,若AB为垂直于x轴的动弦,直线l:x=4与x轴交于点N,直线AF与BN交于点M(x0,y0).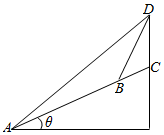 如图所示,在一个坡度一定的山坡AC的顶上有一高度为25m的建筑物CD,为了测量该山坡相对于水平地面的坡角θ,在山坡的A处测得∠DAC=15°,沿山坡前进50m到达B处,又测得∠DBC=45°,根据以上数据可得cosθ=$\sqrt{3}$-1.
如图所示,在一个坡度一定的山坡AC的顶上有一高度为25m的建筑物CD,为了测量该山坡相对于水平地面的坡角θ,在山坡的A处测得∠DAC=15°,沿山坡前进50m到达B处,又测得∠DBC=45°,根据以上数据可得cosθ=$\sqrt{3}$-1.