题目内容
棱长为2的正方体ABCD-A1B1C1D1中,M、N两点分别为棱B1C1、C1D1的中点,那么点C到面DBMN的距离为______.
设点C到面DBMN,即面BMN的距离为h,根据三棱锥的体积公式得:VC-MNB=VN-BMC
∴
×
×
×
h=
×
×2×2×1
∴h=
.
故答案为:
.
∴
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
3
| ||
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
∴h=
| 4 |
| 3 |
故答案为:
| 4 |
| 3 |

练习册系列答案
相关题目
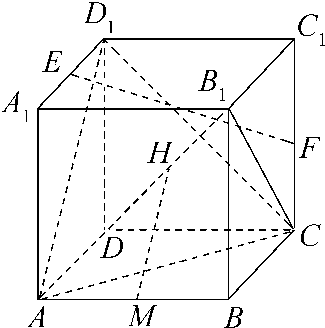 如图,在棱长为2的正方体ABCD-A1B1C1D1中,E、F、M、H分别为A1D1、CC1、AB、DB1的中点.
如图,在棱长为2的正方体ABCD-A1B1C1D1中,E、F、M、H分别为A1D1、CC1、AB、DB1的中点.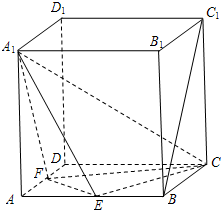 (2007•静安区一模)(文)如图,在棱长为2的正方体ABCD-A1B1C1D1中,点E、F分别是棱AB、AD的中点.求:
(2007•静安区一模)(文)如图,在棱长为2的正方体ABCD-A1B1C1D1中,点E、F分别是棱AB、AD的中点.求: