题目内容
若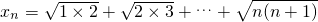 (n为正整数),
(n为正整数),
求证:不等式 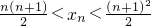 对一切正整数n恒成立.
对一切正整数n恒成立.
证明:∵
∴

即:
∴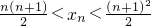 .
.
∴不等式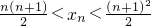 对一切正整数n恒成立..
对一切正整数n恒成立..
分析:先对式子: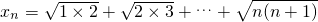 的通项进行放缩:
的通项进行放缩: ,再左右两边分别求和,即可证得结论.
,再左右两边分别求和,即可证得结论.
点评:本题考查不等式的证明(关键是去掉根式),以及数列求和、及放缩法.

∴


即:

∴
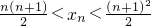 .
.∴不等式
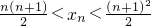 对一切正整数n恒成立..
对一切正整数n恒成立..分析:先对式子:
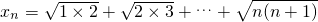 的通项进行放缩:
的通项进行放缩: ,再左右两边分别求和,即可证得结论.
,再左右两边分别求和,即可证得结论.点评:本题考查不等式的证明(关键是去掉根式),以及数列求和、及放缩法.

练习册系列答案
相关题目