题目内容
已知椭圆C: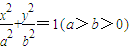 ,过点B(0,1),离心率为
,过点B(0,1),离心率为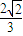 .
.(Ⅰ)求椭圆C的方程;
(Ⅱ)是否存在过点P(0,2)的直线l与椭圆交于M,N两个不同的点,且使
 成立?若存在,求出直线l的方程;若不存在,请说明理由.
成立?若存在,求出直线l的方程;若不存在,请说明理由.
【答案】分析:(Ⅰ)根据椭圆过点B(0,1),离心率为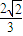 ,即可求得椭圆C的方程;
,即可求得椭圆C的方程;
(Ⅱ)根据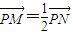 ,可得点M为PN的中点,再分类讨论,将直线方程与椭圆方程联立,利用韦达定理,即可求得直线l的方程.
,可得点M为PN的中点,再分类讨论,将直线方程与椭圆方程联立,利用韦达定理,即可求得直线l的方程.
解答:解:(Ⅰ)由题意可知b=1,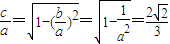 ,解得a2=9
,解得a2=9
故椭圆M的方程为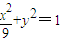 …(4分)
…(4分)
(Ⅱ)∵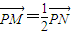 ,∴点M为PN的中点,
,∴点M为PN的中点,
设M(x1,y1),N(x2,y2),则 x2=2x1①…(5分)
(1)当直线的斜率k不存在时,M(0,1),N(0,-1),P(0,2),不符合条件,此时直线方程不存在.…(7分)
(2)当直线的斜率存在时,设直线的方程为y=kx+2
由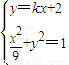 ,消去y 得(9k2+1)x2+36kx+27=0
,消去y 得(9k2+1)x2+36kx+27=0
由△=(36k)2-4•(9k2+1)•27>0,解得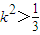 (*) …(9分)
(*) …(9分)
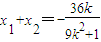 ②,
②,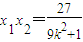 ③
③
由①②③可得消去x1,x2,可得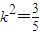 ,故
,故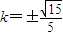 …(13分)
…(13分)
综上可知:存在这样直线l的方程为: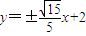 …(14分)
…(14分)
点评:本题考查椭圆的标准方程,考查直线与椭圆的位置关系,考查分类讨论的数学思想,正确运用韦达定理是关键.
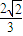 ,即可求得椭圆C的方程;
,即可求得椭圆C的方程;(Ⅱ)根据
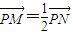 ,可得点M为PN的中点,再分类讨论,将直线方程与椭圆方程联立,利用韦达定理,即可求得直线l的方程.
,可得点M为PN的中点,再分类讨论,将直线方程与椭圆方程联立,利用韦达定理,即可求得直线l的方程.解答:解:(Ⅰ)由题意可知b=1,
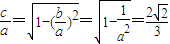 ,解得a2=9
,解得a2=9故椭圆M的方程为
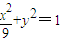 …(4分)
…(4分)(Ⅱ)∵
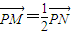 ,∴点M为PN的中点,
,∴点M为PN的中点,设M(x1,y1),N(x2,y2),则 x2=2x1①…(5分)
(1)当直线的斜率k不存在时,M(0,1),N(0,-1),P(0,2),不符合条件,此时直线方程不存在.…(7分)
(2)当直线的斜率存在时,设直线的方程为y=kx+2
由
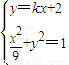 ,消去y 得(9k2+1)x2+36kx+27=0
,消去y 得(9k2+1)x2+36kx+27=0由△=(36k)2-4•(9k2+1)•27>0,解得
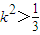 (*) …(9分)
(*) …(9分)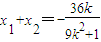 ②,
②,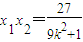 ③
③由①②③可得消去x1,x2,可得
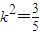 ,故
,故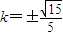 …(13分)
…(13分)综上可知:存在这样直线l的方程为:
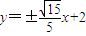 …(14分)
…(14分)点评:本题考查椭圆的标准方程,考查直线与椭圆的位置关系,考查分类讨论的数学思想,正确运用韦达定理是关键.

练习册系列答案
相关题目
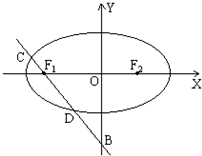 已知椭圆
已知椭圆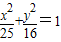 ,过点(3,0)的且斜率为
,过点(3,0)的且斜率为 的直线被C所截线段的中点坐标为( )
的直线被C所截线段的中点坐标为( )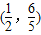
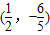
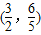
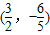
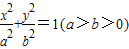 ,过点(-
,过点(-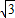 ,
, )离心率e=
)离心率e=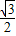 .
. ,过点P(4,0)且不与坐标轴垂直的直线l交椭圆C于A,B两点,设点A关于x轴的对称点为A1
,过点P(4,0)且不与坐标轴垂直的直线l交椭圆C于A,B两点,设点A关于x轴的对称点为A1