题目内容
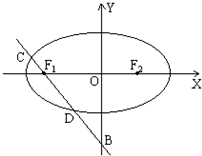 已知椭圆
已知椭圆| x2 | 2 |
(1)试确定直线l的斜率k的取值范围;
(2)若直线l经过椭圆的左焦点F1,椭圆的右焦点为F2,求△CDF2的面积.
分析:(1)设出直线l的方程,联立椭圆方程,利用直线和椭圆相交两个点,可得△>0,由此可求直线l的斜率k的取值范围;
(2)求出直线l的方程,点F2(1,0)到l的距离,计算|CD|,即可求得面积.
(2)求出直线l的方程,点F2(1,0)到l的距离,计算|CD|,即可求得面积.
解答:解:(1)设直线l:y=kx-2,联立椭圆方程,消去y得:(1+2k2)x2-8kx+6=0(*)
由于直线和椭圆相交两个点,故△=8(2k2-3)>0,得:k>
或k<
.
(2)直线l经过点B(0,-2)和F1(-1,0),所以l:2x+y+2=0
点F2(1,0)到l的距离d=
联立直线和椭圆方程得:9x2+16x+6=0,
∴|CD|=|x1-x2|
=
∴S△=
|CD|d=
.
由于直线和椭圆相交两个点,故△=8(2k2-3)>0,得:k>
| ||
| 2 |
| ||
| 2 |
(2)直线l经过点B(0,-2)和F1(-1,0),所以l:2x+y+2=0
点F2(1,0)到l的距离d=
| 4 | ||
|
联立直线和椭圆方程得:9x2+16x+6=0,
∴|CD|=|x1-x2|
| 1+k2 |
| 10 |
| 9 |
| 2 |
∴S△=
| 1 |
| 2 |
| 4 |
| 9 |
| 10 |
点评:本题考查直线与椭圆的位置关系,考查三角形面积的计算,考查学生的计算能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
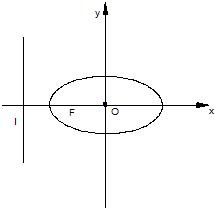 已知椭圆
已知椭圆 已知椭圆
已知椭圆