题目内容
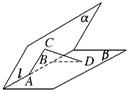二面角α-l-β为60°，A、B是棱l上的两点，AC、BD分别在半平面α、β内，AC⊥l，BD⊥l，且AB=AC=a，BD=2a，则CD的长为（ ）
| A、2a | ||
B、
| ||
| C、a | ||
D、
|
分析：先利用现有图形构造出一个四棱柱，再利用空间向量进行计算，欲求CD的长，即求向量
的模，也就是求向量
+
+
的模，利用向量的数量积运算即可求得．
| CD |
| CA |
| AB |
| BD |
解答：
解：∵AC⊥l，BD⊥l，
∴＜
，
＞=60°，且
•
=0，
•
=0，
∴
=
+
+
，
∴|
|=
=
=2a．
答案：A
解：∵AC⊥l，BD⊥l，∴＜
| AC |
| BD |
| AC |
| BA |
| AB |
| BD |
∴
| CD |
| CA |
| AB |
| BD |
∴|
| CD |
(
|
=
| a2+a2+(2a)2+2a•2acos120° |
答案：A
点评：本题主要考查了空间向量，以及空间几何体的概念、空间想象力，属于基础题．
练习册系列答案
相关题目
已知α-l-β是大小为45°的二面角，C为二面角内一定点，且到半平面α和β的距离分别为
和6，A、B分别是半平面α，β内的动点，则△ABC周长的最小值为（ ）
| 2 |
A、6
| ||
B、5
| ||
| C、15 | ||
D、10
|
如图，在二面角α-l-β的棱l上有A，B两点，直线AC，BD分别在这个二面角的两个半平面内，且都垂直于AB，若