题目内容
(1)求证:
-
<
-2;
(2)已知函数f(x)=ex+
,用反证法证明方程f(x)=0没有负数根.
| 7 |
| 6 |
| 5 |
(2)已知函数f(x)=ex+
| x-2 |
| x+1 |
证明:(1)要证
-
<
-2
只需证(
-
)2<(
-2)2
只需证 13-2
<9-4
即证2+2
<
只需证24+8
<42
只需证 4
<9 即证80<81
上式显然成立,命题得证.
(2)设存在x0<0(x0≠-1),使f(x0)=0,则e x0=-
由于0<e x0<1得0<-
<1,解得
<x0<2,
与已知x0<0矛盾,因此方程f(x)=0没有负数根.
| 7 |
| 6 |
| 5 |
只需证(
| 7 |
| 6 |
| 5 |
只需证 13-2
| 42 |
| 5 |
| 5 |
| 42 |
只需证24+8
| 5 |
只需证 4
| 5 |
上式显然成立,命题得证.
(2)设存在x0<0(x0≠-1),使f(x0)=0,则e x0=-
| x0-2 |
| x0+1 |
由于0<e x0<1得0<-
| x0-2 |
| x0+1 |
| 1 |
| 2 |
与已知x0<0矛盾,因此方程f(x)=0没有负数根.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
 上的函数
上的函数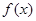 ,若存在闭区间
,若存在闭区间 和常数
和常数 ,使得对任意的
,使得对任意的 都有
都有 ,且对任意的
,且对任意的 都有
都有 恒成立,则称函数
恒成立,则称函数 是
是 上的“U型”函数;
上的“U型”函数; 对一切的
对一切的 恒成立,
恒成立, 的取值范围;
的取值范围; 是区间
是区间 上的“U型”函数,求实数
上的“U型”函数,求实数 和
和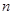 的值.
的值.