题目内容
(本小题满分12分)已知函数f(x)=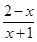 ;
;
(Ⅰ)证明:函数f(x)在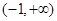 上为减函数;
上为减函数;
(Ⅱ)是否存在负数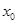 ,使得
,使得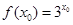 成立,若存在求出
成立,若存在求出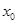 ;若不存在,请说明理由。
;若不存在,请说明理由。
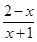 ;
;(Ⅰ)证明:函数f(x)在
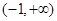 上为减函数;
上为减函数;(Ⅱ)是否存在负数
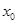 ,使得
,使得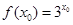 成立,若存在求出
成立,若存在求出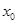 ;若不存在,请说明理由。
;若不存在,请说明理由。解:(1)任取
 ,且
,且
∵
 …………4分
…………4分∴函数
 在
在 上为减函数 ………………………6分
上为减函数 ………………………6分另解:如果应用导数证明请相应给分

(2)不存在 ……………………………………………………7分
假设存在负数
 ,使得
,使得 成立,则
成立,则 即
即

 ……………10分
……………10分 与
与 矛盾,
矛盾, 所以不存在负数
 ,使得
,使得 成立。 ………………12分
成立。 ………………12分另解:
 ,由
,由 得:
得:  或
或 但
但 ,
,所以不存在。
略

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
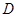 上的函数
上的函数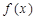 ,如果满足:对任意
,如果满足:对任意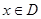 ,存在常数
,存在常数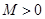 ,都有
,都有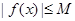 成立,则称
成立,则称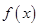 是
是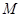 称为函数
称为函数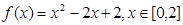 是否是有界函数,请写出详细判断过程;
是否是有界函数,请写出详细判断过程;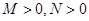 ,若
,若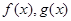 在
在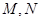 为上界,
为上界,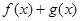 在
在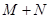 为上界;
为上界;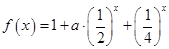 在
在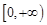 上是以3为上界的有界函数,
上是以3为上界的有界函数,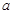 的取值范围.
的取值范围. 在定义域
在定义域 上是减函数,且
上是减函数,且 ,则实数
,则实数 的取值范围为 ▲
的取值范围为 ▲ 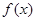 是定义在
是定义在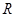 上的偶函数,在区间
上的偶函数,在区间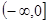 上是减函数,且
上是减函数,且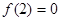 ,则使
,则使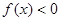 的
的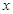 的取值范围是( )
的取值范围是( )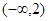
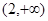
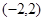
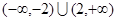
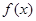 是定义在
是定义在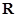 上的增函数,且对于任意的
上的增函数,且对于任意的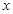 都有
都有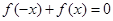 恒成立. 如果实数
恒成立. 如果实数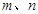 满足不等式
满足不等式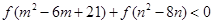 ,那么
,那么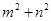 的取值范围是
的取值范围是 ,1)
,1)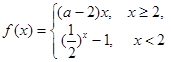 满足对任意的实数
满足对任意的实数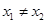 都有
都有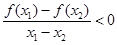 成立,则实数
成立,则实数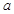 的取值范围为( )
的取值范围为( )

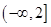
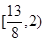
 在
在 上单调递减,则
上单调递减,则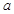 的取值组成的集合是_______。
的取值组成的集合是_______。 在区间[3,6]上的最大值是________;最小值是__________;
在区间[3,6]上的最大值是________;最小值是__________;