题目内容
函数f(x)=x+
的单调递减区间是( )
| 2 |
| x |
A、(0,
| ||||
B、[-
| ||||
C、(0,
| ||||
D、(0,
|
分析:由函数的单调性定义,本题作差 f(x1)-f(x2),变形得到(x1-x2)•
,分两种情况进行讨论可以得到函数的单调区间,要注意两个单调减区间(0,
],[-
, 0),不能写成(0,
]∪[-
, 0)的形式
| x1x2-2 |
| x1x2 |
| 2 |
| 2 |
| 2 |
| 2 |
解答:解:设0<x1<x2,则
f(x1)-f(x2)=(x1+
)-(x2+
)
=(x1-x2)+(
-
)
=(x1-x2)•
因为0<x1<x2,所以x1-x2<0,x1•x2>0,
所以当0<x1<x2≤
时,x1•x2-2<0,所以
<0
所以:f(x1)-f(x2)>0,即f(x1)>f(x2)
所以f(x)在(0,
]上是减函数.
同理可证:f(x)在[-
,0)上也是减函数.
故选:D
f(x1)-f(x2)=(x1+
| 2 |
| x1 |
| 2 |
| x2 |
=(x1-x2)+(
| 2 |
| x1 |
| 2 |
| x2 |
=(x1-x2)•
| x1x2-2 |
| x1x2 |
因为0<x1<x2,所以x1-x2<0,x1•x2>0,
所以当0<x1<x2≤
| 2 |
| x1x2-2 |
| x1x2 |
所以:f(x1)-f(x2)>0,即f(x1)>f(x2)
所以f(x)在(0,
| 2 |
同理可证:f(x)在[-
| 2 |
故选:D
点评:本题考查函数的单调性以及单调区间的求法,利用定义解答求单调区间的时候,要注意x1,x2的任意性,本题中求解区间
需要分0<x1<x2≤
和-
≤x1<x2<0进行讨论.
需要分0<x1<x2≤
| 2 |
| 2 |

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案
相关题目
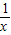 是奇函数”的证明不是综合法的是( )
是奇函数”的证明不是综合法的是( )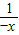 =-(x+
=-(x+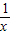 )=-f(x),∴f(x)是奇函数
)=-f(x),∴f(x)是奇函数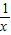 +(-x)+(-
+(-x)+(-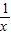 )=0,∴f(x)=-f(-x),∴f(x)是奇函数
)=0,∴f(x)=-f(-x),∴f(x)是奇函数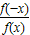 =
=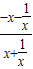 =-1,∴f(-x)=-f(x),∴f(x)是奇函数
=-1,∴f(-x)=-f(x),∴f(x)是奇函数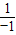 =-2,又f(1)=1+
=-2,又f(1)=1+ =2
=2