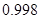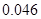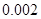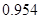题目内容
设有关于x的一元二次方程x2+2ax+b2="0." (l)若a是从0,1,2,3四个数中任取的一个数,b是从0,1,2三个数中任取的一个数,求方程有实根的概率;(2)若a是从区间[0,t+1]任取的一个数,b是从区间[0,t]任取的一个数,其中t满足2≤t≤3,求方程有实根的概率,并求出其概率的最大值.
(1) ;(2)
;(2) .
.
 ;(2)
;(2) .
.试题分析:(1)本小题为古典概型求概率的问题,先求出a与b构成的实数对(a,b)总个数即基本事件的总数,再一一进行检验符合
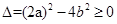 的实数对即可求出其概率;(2)本小题为几何概型求概率的问题,由0≤a≤t+1,0≤b≤t利用线性规划的知识(a看直角坐标系中的x,b看成直角坐标系中的y)可画出如下图的矩形,又a≥b(即为y≤x区域)则符合条件的阴影部分区域为梯形,因此所求的概率为
的实数对即可求出其概率;(2)本小题为几何概型求概率的问题,由0≤a≤t+1,0≤b≤t利用线性规划的知识(a看直角坐标系中的x,b看成直角坐标系中的y)可画出如下图的矩形,又a≥b(即为y≤x区域)则符合条件的阴影部分区域为梯形,因此所求的概率为 ,其次根据t的范围利用不等式的性质求出P的范围即可找到其最大值.
,其次根据t的范围利用不等式的性质求出P的范围即可找到其最大值.试题解析:(1)总的基本事件有12个,即a,b构成的实数对(a,b)有(0,0),(0,1),(0,2),(1,0),(1,1),(1,2),(2,0),(2,1),(2,2),(3,0),(3,1),(3,2).设事件A为“方程有实根”,包含的基本事件有(0,0),(1,0),(1,1),(2,0),(2,1),(2,2),(3,0),(3,1),(3,2)共9个,所以事件A的概率为P(A)=
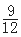 =
= ;
;(2)a,b构成的实数对(a,b)满足条件有0≤a≤t+1,0≤b≤t,a≥b,设事件B为“方程有实根”,则此事件满足几何概型. 如图,

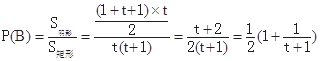 ,∵2≤t≤3,∴3≤t+1≤4,即
,∵2≤t≤3,∴3≤t+1≤4,即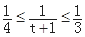 ,所以
,所以 ,即
,即 ≤P(B)≤
≤P(B)≤ ,所以其概率的最大值为
,所以其概率的最大值为 .
.
练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
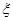 为取出的4个球中红球的个数,求
为取出的4个球中红球的个数,求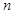 及天数如下表:
及天数如下表:
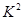 的一个可能取值为( )
的一个可能取值为( )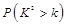
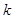
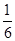
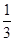
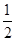
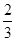
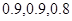 ,若至少有两枚导弹命中目标方可将其摧毁,则目标被摧毁的概率为( )
,若至少有两枚导弹命中目标方可将其摧毁,则目标被摧毁的概率为( )