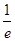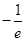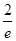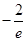题目内容
(本小题12分)设函数
(1)求函数 的单调区间;
的单调区间;
(2)求 在
在 上的最小值;
上的最小值;

(1)求函数
 的单调区间;
的单调区间;(2)求
 在
在 上的最小值;
上的最小值; (1)函数 的增区间为
的增区间为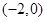 和
和 ,减区间为
,减区间为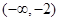 和
和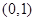 .
.
(2) 在
在 上的最小值为
上的最小值为
 的增区间为
的增区间为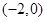 和
和 ,减区间为
,减区间为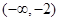 和
和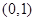 .
.(2)
 在
在 上的最小值为
上的最小值为
本试题主要是考查了导数在研究函数中的 运用。求解函数的单调性以及函数的最值的综合运用。
(1)首先分析定义域,然后求解导数,令导数为零,得到导函数与x轴 的交点,然后分析导数大于零或者小于零的解得到结论。
(2)根据第一问的结论,结合函数的单调性,可知函数在给定区间的最值问题。
解:(1) ,
,
令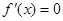 ,可得
,可得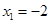 ,
,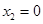 ,
,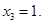
当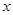 变化时,
变化时, ,
, 的变化情况如下表:
的变化情况如下表:
 函数
函数 的增区间为
的增区间为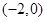 和
和 ,减区间为
,减区间为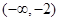 和
和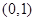 .
.
(2)当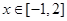 时,
时,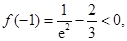
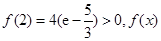 极小值
极小值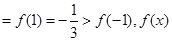 极大值
极大值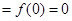 .
.
所以 在
在 上的最小值为
上的最小值为
(1)首先分析定义域,然后求解导数,令导数为零,得到导函数与x轴 的交点,然后分析导数大于零或者小于零的解得到结论。
(2)根据第一问的结论,结合函数的单调性,可知函数在给定区间的最值问题。
解:(1)
 ,
,令
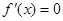 ,可得
,可得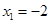 ,
,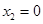 ,
,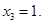
当
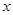 变化时,
变化时, ,
, 的变化情况如下表:
的变化情况如下表: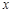 | 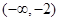 | 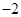 | 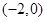 | 0 | 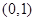 | 1 |  |
 | - | 0 | + | 0 | - | 0 | + |
 |  | 极小值 | 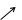 | 极大值 |  | 极小值 | 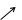 |
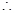 函数
函数 的增区间为
的增区间为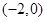 和
和 ,减区间为
,减区间为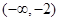 和
和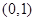 .
.(2)当
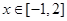 时,
时,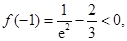
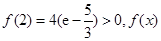 极小值
极小值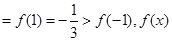 极大值
极大值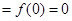 .
.所以
 在
在 上的最小值为
上的最小值为

练习册系列答案
相关题目
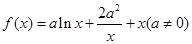 .
.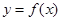 在点
在点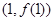 处的切线与直线
处的切线与直线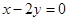 垂直,求实数
垂直,求实数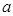 的值;
的值;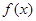 的单调性;
的单调性;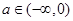 时,记函数
时,记函数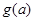 ,求证:
,求证: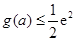 .
. 在点
在点 处的切线方程是
处的切线方程是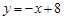 ,则
,则 +
+ = .
= .
 在
在 处的切线方程为 .
处的切线方程为 .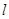 是曲线
是曲线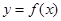 在
在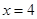 处的切线,则
处的切线,则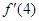 =
= 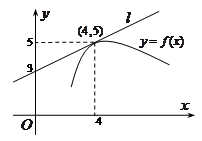
 在区间
在区间 的导函数
的导函数 ,
, ,若在区间
,若在区间 恒成立,则称函数
恒成立,则称函数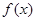 在区间
在区间 ,若当实数
,若当实数 满足
满足 时,函数
时,函数 的最大值为( )
的最大值为( )

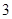

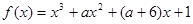 有极大值和极小值,则a的取值范围是( )
有极大值和极小值,则a的取值范围是( )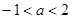
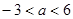
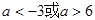

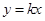 是曲线
是曲线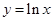 的切线,则k的值为( )
的切线,则k的值为( )