题目内容
已知椭圆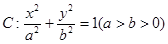 过点
过点 ,且离心率
,且离心率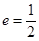 .
.
(1)求椭圆 的标准方程;
的标准方程;
(2)若直线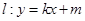 与椭圆
与椭圆 相交于
相交于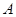 ,
,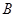 两点(
两点(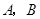 不是左右顶点),椭圆的右顶点为
不是左右顶点),椭圆的右顶点为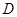 ,且满足
,且满足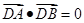 ,试判断直线是否过定点,若过定点,求出该定点的坐标;若不过定点,请说明理由.
,试判断直线是否过定点,若过定点,求出该定点的坐标;若不过定点,请说明理由.
(1)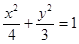 ;(2)
;(2) .
.
解析试题分析:(1)本小题通过待定系数法列出两个关于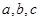 的方程,通过解方程组求出椭圆的方程,包含着二次方的运算需掌握;(2)本小题是直线与椭圆的位置关系的问题,这类题目的常用思路就是联立直线方程和椭圆方程通过消元得到一个一元二次方程,确定判别式的情况,正确书写、利用韦达定理,由
的方程,通过解方程组求出椭圆的方程,包含着二次方的运算需掌握;(2)本小题是直线与椭圆的位置关系的问题,这类题目的常用思路就是联立直线方程和椭圆方程通过消元得到一个一元二次方程,确定判别式的情况,正确书写、利用韦达定理,由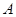 ,
,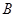 两点(
两点(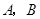 不是左右顶点),椭圆的右顶点为
不是左右顶点),椭圆的右顶点为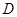 ,且满足
,且满足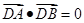 ,根据向量的数量积为零,可得到关于两个根的等式,再利用韦达定理可得关于
,根据向量的数量积为零,可得到关于两个根的等式,再利用韦达定理可得关于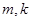 的等式,从而就可得出相应的结论.
的等式,从而就可得出相应的结论.
试题解析:(1)
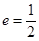
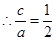 即
即
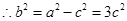
∴椭圆方程为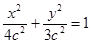 4分
4分
又点 在椭圆上,
在椭圆上,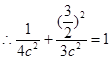 解得
解得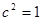
∴椭圆的方程为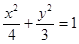 6分
6分
(2)设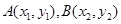 ,由
,由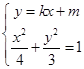 得
得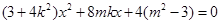
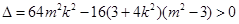 ,
,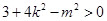
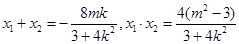 8分
8分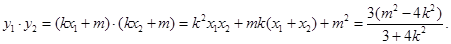
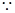
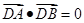
所以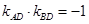 ,又椭圆的右顶点
,又椭圆的右顶点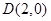
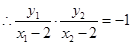 ,
,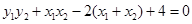
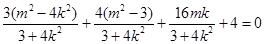
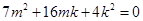 ,解得 10分
,解得 10分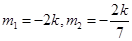 ,且满足
,且满足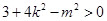
当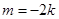 时,
时,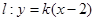 ,直线过定点
,直线过定点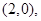 与已知矛盾 12分
与已知矛盾 12分
当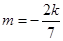 时,
时,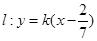 ,直线过定点
,直线过定点
综上可知,当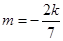 时,直线过定点,定点坐标为
时,直线过定点,定点坐标为 14分.
14分.
考点:1.直线与椭圆的位置关系;2.韦达定理;3.平面向量的数量积;4.过定点的问题;5.直线与椭圆的综合问题.

练习册系列答案
相关题目
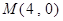 、
、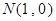 ,若动点
,若动点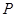 满足
满足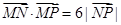 .
.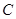 的方程;
的方程;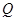 ,使点
,使点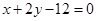 的距离最小.
的距离最小. ,且过点P(4,-
,且过点P(4,-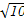 ).
).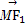 ·
·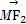 =0.
=0.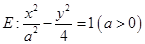 的中心为原点
的中心为原点 ,左、右焦点分别为
,左、右焦点分别为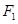 、
、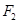 ,离心率为
,离心率为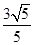 ,点
,点 是直线
是直线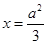 上任意一点,点
上任意一点,点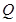 在双曲线
在双曲线 上,且满足
上,且满足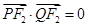 .
.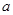 的值;
的值;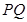 与直线
与直线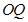 的斜率之积是定值;
的斜率之积是定值; ,过点
,过点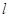 与双曲线右支交于不同的两点
与双曲线右支交于不同的两点 、
、 ,在线段
,在线段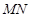 上去异于点
上去异于点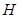 ,满足
,满足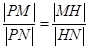 ,证明点
,证明点 =1(a>b>0)右焦点F2的直线交椭圆于A,B两点,F1为其左焦点,已知△AF1B的周长为8,椭圆的离心率为
=1(a>b>0)右焦点F2的直线交椭圆于A,B两点,F1为其左焦点,已知△AF1B的周长为8,椭圆的离心率为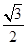 .
.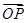 ⊥
⊥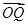 ?若存在,求出该圆的方程;若不存在,请说明理由.
?若存在,求出该圆的方程;若不存在,请说明理由.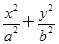 =1(a>b>0)的两个焦点分别为F1,F2,离心率为
=1(a>b>0)的两个焦点分别为F1,F2,离心率为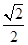 ,且过点(2,
,且过点(2,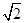 ).
).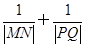 为定值.
为定值.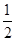 .
. ,试判断|PM|+|PQ|是否存在最小值,若存在,求出其最小值,若不存在,请说明理由;
,试判断|PM|+|PQ|是否存在最小值,若存在,求出其最小值,若不存在,请说明理由;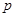 :方程
:方程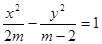 表示焦点在
表示焦点在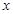 轴上的双曲线。命题
轴上的双曲线。命题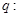 曲线
曲线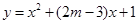 与
与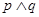 为假命题,
为假命题,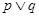 为真命题,求实数
为真命题,求实数 的取值范围。
的取值范围。