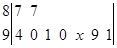题目内容
废品率
和每吨生铁成本
(元)之间的回归直线方程为
，这表明 （ ）
A．与 的相关系数为2 |
| B．与的关系是函数关系的充要条件是相关系数为1 |
| C．废品率每增加1%，生铁成本增加258元 |
| D．废品率每增加1%，生铁成本平均每吨增加2元 |
D
解析试题分析：选项
回归直线中
的系数叫回归系数，相关系数是
， 
，所以不正确 ；
选项
，当相关系数
时所有点都在同一直线上反之亦成立，但是函数关系不一定是线性关系所以不正确；选项
，
，因为
所以
所以 不正确，
正确.
考点：统计概念，线性相关，回归系数.
学校为了了解高二年级教学情况，对全省班、实验班、普通班、中加班的学生做分层抽样调查．假设我校高二年级总人数为N，其中全省班有学生96人．若在全省班、实验班、普通班、中加班抽取的人数分别为12,21,25,43，则总人数N为 ( )
| A．801； | B．808； | C．853； | D．912. |
如图是某赛季甲、乙两名篮球运动员每场比赛得分的茎叶图，则甲、乙两人这几场比赛得分的中位数之和是（ ）
| A．65 | B．64 | C．63 | D．62 |
对某班级
名学生学习数学与学习物理的成绩进行调查，得到如下表所示：
| | 数学成绩较好 | 数学成绩一般 | 合计 |
| 物理成绩较好 | 18 | 7 | 25 |
| 物理成绩一般 | 6 | 19 | 25 |
| 合计 | 24 | 26 | 50 |
，解得
 | 0.050 | 0.010 | 0.001 |
 | 3.841 | 6.635 | 10.828 |
参照附表，得到的正确结论是（ ）
（A）在犯错误的概率不超过
的前提下，认为“数学成绩与物理成绩有关”（B）在犯错误的概率不超过
的前提下，认为“数学成绩与物理成绩无关”（C）有
的把握认为“数学成绩与物理成绩有关”（D）有
以上的把握认为“数学成绩与物理成绩无关” 某校高三2班有48名学生进行了一场投篮测试，其中男生28人，女生20人．为了了解其投篮成绩，甲、乙两人分别对全班的学生进行编号（1~48号），并以不同的方法进行数据抽样，其中一人用的是系统抽样，另一人用的是分层抽样．若此次投篮考试的成绩大于或等于80分视为优秀，小于80分视为不优秀，以下是甲、乙两人分别抽取的样本数据：
（Ⅰ）从甲抽取的样本数据中任取两名同学的投篮成绩，记“抽到投篮成绩优秀”的人数为X，求X的分布列和数学期望；
（Ⅱ）请你根据乙抽取的样本数据完成下列2×2列联表，判断是否有95%以上的把握认为投篮成绩和性别有关？
（Ⅲ）判断甲、乙各用何种抽样方法，并根据（Ⅱ）的结论判断哪种抽样方法更优？说明理由.
下面的临界值表供参考：
 | 0.15 | 0.10 | 0.05 | 0.010 | 0.005 | 0.001 |
 | 2.072 | 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
，其中
） 某商品的销售量
（件）与销售价格
（元/件）存在线性相关关系，根据一组样本数据
，用最小二乘法建立的回归方程为
则下列结论正确的是（ ）
| A．与具有正的线性相关关系 |
B．若 表示变量与之间的线性相关系数，则 |
| C．当销售价格为10元时，销售量为100件 |
| D．当销售价格为10元时，销售量为100件左右 |
S大学艺术系表演专业的报考人数连创新高，2010年报名刚结束，某考生想知道这次报考该专业的人数．已知该专业考生的考号是按0001,0002，…的顺序从小到大依次排列的，他随机了解了50名考生的考号，经计算，这50个考号的和是25025， 估计2010年报考S大学艺术系表演专业的考生大约有( )
| A．500人 | B．1000人 | C．1500人 | D．2000人 |
个得分去掉
个最高分，去掉
个剩余分数的平均分为
，现场做的
表示：
