题目内容
(本小题12分)已知三次函数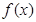 的导函数
的导函数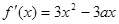 ,
,
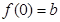 ,(
,(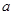 ,
,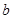
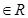 ).
).
(1)若曲线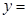
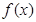 在点(
在点(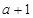 ,
,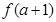 )处切线的斜率为12,求
)处切线的斜率为12,求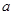 的值;
的值;
(2)若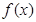 在区间[-1,1]上的最小值,最大值分别为-2和1,且
在区间[-1,1]上的最小值,最大值分别为-2和1,且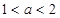 ,求函数
,求函数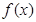 的解析式.
的解析式.
【答案】
(1)a=3;(2)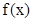 =
=
【解析】第一问中利用导数的几何意义可得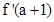 =12
=12
∴ 解得a的值
解得a的值
第二问∵ ,
,
∴ …5分
…5分
由 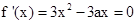 利用导数判定单调性得到。
利用导数判定单调性得到。
解:(1)由导数的几何意义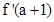 =12 ……………1分
=12 ……………1分
∴ ……………2分
……………2分
∴ 3a=9 ∴ a=3 ………………………3分
(2)∵ ,
,
∴ …5分
…5分
由 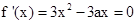 得
得 ,
,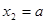
∵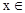 [-1,1],1<a<2
[-1,1],1<a<2
∴ 当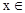 [-1,0)时,
[-1,0)时, ,
,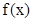 递增;
递增;
当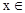 (0,1]时,
(0,1]时, ,
,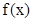 递减。……………8分
递减。……………8分
∴ 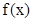 在区间[-1,1]上的最大值为f(0)
在区间[-1,1]上的最大值为f(0)
∵ 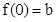 ,∴ b=1 ……………………10分
,∴ b=1 ……………………10分
∵ 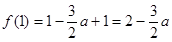 ,
,
∴ f(-1)<f(1) ∴
f(-1)是函数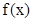 的最小值,
的最小值,
∴ -3/2 a=-2 ∴ a=4/3
∴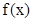 =
=

练习册系列答案
相关题目
 中,
中, 。
。 中,
中, ,求数列
,求数列 项和
项和 .
. 轴上的抛物线与直线
轴上的抛物线与直线 交于P、Q两点,|PQ|=
交于P、Q两点,|PQ|= ,求抛物线的方程
,求抛物线的方程 ;
; 过
过 且与圆C相切,求直线
且与圆C相切,求直线 ,使直线
,使直线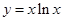
 处的切线方程。
处的切线方程。