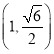Question

【题目】给出以下四个结论：

①过点，在两轴上的截距相等的直线方程是；

②若是等差数列的前n项和，则；

③在中，若，则是等腰三角形；

④已知，，且，则的最大值是2.

其中正确的结论是________（写出所有正确结论的番号）.

Answer 1

【答案】②④

【解析】

①中满足题意的直线还有，②中根据等差数列前项和的特点，得到，③中根据同角三角函数关系进行化简计算，从而进行判断，④中根据基本不等式进行判断.

①中过点，在两轴上的截距相等的直线还可以过原点，即两轴上的截距都为，即直线，所以错误；

②中是等差数列的前n项和，根据等差数列前项和的特点，，是一个不含常数项的二次式，从而得到，即，所以正确；

③中在中，若，则可得，

所以可得或，所以可得或，从而得到为直角三角形或等腰三角形，所以错误；

④中因为，，且，

由基本不等式，得到，

所以，当且仅当，即时，等号成立.

所以，

即的最大值是，所以正确.

故答案为：②④