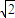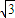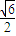题目内容
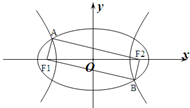
 如图F1、F2是椭圆C1:
如图F1、F2是椭圆C1: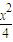 +y2=1与双曲线C2的公共焦点A、B分别是C1、C2在第二、四象限的公共点,若四边形AF1BF2为矩形,则C2的离心率是( )
+y2=1与双曲线C2的公共焦点A、B分别是C1、C2在第二、四象限的公共点,若四边形AF1BF2为矩形,则C2的离心率是( )A.

B.
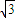
C.

D.
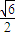
【答案】分析:不妨设|AF1|=x,|AF2|=y,依题意 ,解此方程组可求得x,y的值,利用双曲线的定义及性质即可求得C2的离心率.
,解此方程组可求得x,y的值,利用双曲线的定义及性质即可求得C2的离心率.
解答:解:设|AF1|=x,|AF2|=y,∵点A为椭圆C1: +y2=1上的点,
+y2=1上的点,
∴2a=4,b=1,c= ;
;
∴|AF1|+|AF2|=2a=4,即x+y=4;①
又四边形AF1BF2为矩形,
∴ +
+ =
= ,即x2+y2=(2c)2=
,即x2+y2=(2c)2= =12,②
=12,②
由①②得: ,解得x=2-
,解得x=2- ,y=2+
,y=2+ ,设双曲线C2的实轴长为2a,焦距为2c,
,设双曲线C2的实轴长为2a,焦距为2c,
则2a=,|AF2|-|AF1|=y-x=2 ,2c=2
,2c=2 =2
=2 ,
,
∴双曲线C2的离心率e= =
= =
= .
.
故选D.
点评:本题考查椭圆与双曲线的简单性质,求得|AF1|与|AF2|是关键,考查分析与运算能力,属于中档题.
 ,解此方程组可求得x,y的值,利用双曲线的定义及性质即可求得C2的离心率.
,解此方程组可求得x,y的值,利用双曲线的定义及性质即可求得C2的离心率.解答:解:设|AF1|=x,|AF2|=y,∵点A为椭圆C1:
 +y2=1上的点,
+y2=1上的点,∴2a=4,b=1,c=
 ;
;∴|AF1|+|AF2|=2a=4,即x+y=4;①
又四边形AF1BF2为矩形,
∴
 +
+ =
= ,即x2+y2=(2c)2=
,即x2+y2=(2c)2= =12,②
=12,②由①②得:
 ,解得x=2-
,解得x=2- ,y=2+
,y=2+ ,设双曲线C2的实轴长为2a,焦距为2c,
,设双曲线C2的实轴长为2a,焦距为2c,则2a=,|AF2|-|AF1|=y-x=2
 ,2c=2
,2c=2 =2
=2 ,
,∴双曲线C2的离心率e=
 =
= =
= .
.故选D.
点评:本题考查椭圆与双曲线的简单性质,求得|AF1|与|AF2|是关键,考查分析与运算能力,属于中档题.

练习册系列答案
相关题目
 (2013•浙江)如图F1、F2是椭圆C1:
(2013•浙江)如图F1、F2是椭圆C1: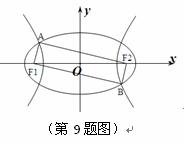
 如图F1、F2是椭圆C1:
如图F1、F2是椭圆C1: +y2=1与双曲线C2的公共焦点A、B分别是C1、C2在第二、四象限的公共点,若四边形AF1BF2为矩形,则C2的离心率是( )
+y2=1与双曲线C2的公共焦点A、B分别是C1、C2在第二、四象限的公共点,若四边形AF1BF2为矩形,则C2的离心率是( )