题目内容
13.y=sin2x+cosxsinx的最大值是$\frac{\sqrt{2}+1}{2}$,最小值是$\frac{-\sqrt{2}+1}{2}$.分析 由条件利用三角恒等变换化简函数的解析式,再根据正弦函数的值域,求得函数的最值.
解答 解:y=sin2x+cosxsinx=$\frac{1-cos2x}{2}$+$\frac{1}{2}$sin2x=$\frac{\sqrt{2}}{2}$sin(2x-$\frac{π}{4}$)+$\frac{1}{2}$,
故它的最大值为$\frac{\sqrt{2}+1}{2}$,它的最小值为$\frac{-\sqrt{2}+1}{2}$,
故答案为:$\frac{\sqrt{2}+1}{2}$;$\frac{-\sqrt{2}+1}{2}$.
点评 本题主要考查三角恒等变换,正弦函数的值域,属于基础题.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
16.设α,β为两个不同的平面,n,m为两条不同的直线,且n?α,m?β,有如下两个命题:
p:若α∥β,则n∥m;
q:若m⊥n,则α⊥β,那么( )
p:若α∥β,则n∥m;
q:若m⊥n,则α⊥β,那么( )
| A. | p∧q是假命题 | B. | p∨q是真命题 | C. | ¬p是假命题 | D. | p∧(¬q)是真命题 |
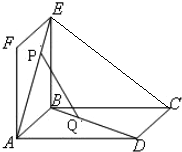 如图:已知有公共边AB的两个全等的矩形ABCD和ABEF不在同一个平面内,P,Q分别是对角线AE,BD上的点,且AP=DQ,求证:PQ∥面CBE.
如图:已知有公共边AB的两个全等的矩形ABCD和ABEF不在同一个平面内,P,Q分别是对角线AE,BD上的点,且AP=DQ,求证:PQ∥面CBE.