题目内容
如图所示，对应关系f是从A到B的映射的是（ ）
分析：根据映射的定义对各项中的对应依此加以验证，可得A、B、C都不能构成从A到B的映射，只有D符合映射的定义，能构成从A到B的映射，由此可得本题的答案．
解答：解：对于A，由于x=9或4时有两个y值与之对应，故f不能构成从A到B的映射，得A不正确；
对于B，由于x=0时没有y值与之对应，故f不能构成从A到B的映射，得B不正确；
对于C，由于x=0时没有y值与之对应，故f不能构成从A到B的映射，得C不正确；
对于D，自变量x=8、4和0都与函数值y=0对应，自变量x=1与函数值y=1对应，
故f可以构成从A到B的映射，得D正确．
故选：D
对于B，由于x=0时没有y值与之对应，故f不能构成从A到B的映射，得B不正确；
对于C，由于x=0时没有y值与之对应，故f不能构成从A到B的映射，得C不正确；
对于D，自变量x=8、4和0都与函数值y=0对应，自变量x=1与函数值y=1对应，
故f可以构成从A到B的映射，得D正确．
故选：D
点评：本题给出几个对应关系，要求找出其中的映射．着重考查了映射的定义及其应用的知识，属于基础题．
练习册系列答案
相关题目
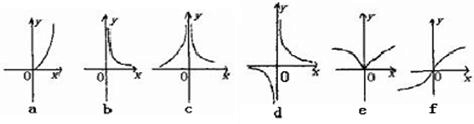
下面六个幂函数的图象如图所示，试建立函数与图象之间的对应关系，其中正确的对应选项是（ ）(1)y=x
；(2)y=x
；(3)y=
；(4)y=x-2；(5)y=x-3；(6)y=x-
．
| 3 |
| 2 |
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 2 |
| A、（1）a，（2）f，（3）c，（4）e，（5）d，（6）b |
| B、（1）a，（2）f，（3）e，（4）c，（5）d，（6）b |
| C、（1）a，（2）b，（3）e，（4）c，（5）d，（6）f |
| D、（1）a，（2）f，（3）d，（4）c，（5）e，（6）b |
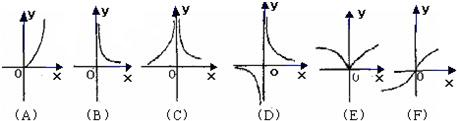
下面六个幂函数的图象如图所示，试建立函数与图象之间的对应关系．（ ）
（1）y=x
；（2）y=x
；（3）y=x
；（4）y=x-2；（5）y=x-3；（6）y=x-
．
（1）y=x
| 3 |
| 2 |
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 2 |
| A、（1）?（A），（2）?（F），（3）?（E），（4）?（C），（5）?（D），（6）?（B） |
| B、（1）?（B），（2）?（E），（3）?（C），（4）?（D），（5）?（A），（6）?（F） |
| C、（1）?（A），（2）?（E），（3）?（B），（4）?（D），（5）?（C），（6）?（F） |
| D、（1）?（B），（2）?（F），（3）?（A），（4）?（C），（5）?（D），（6）?（E） |
15、已知函数f（x）=2x及g（x）=x3的图象如图所示．
