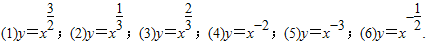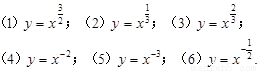题目内容
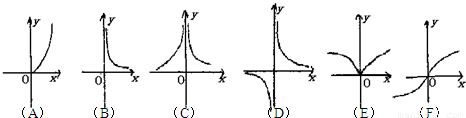
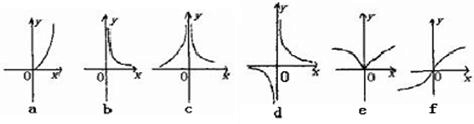
下面六个幂函数的图象如图所示，试建立函数与图象之间的对应关系，其中正确的对应选项是（ ）(1)y=x
；(2)y=x
；(3)y=
；(4)y=x-2；(5)y=x-3；(6)y=x-
．
| 3 |
| 2 |
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 2 |
| A、（1）a，（2）f，（3）c，（4）e，（5）d，（6）b |
| B、（1）a，（2）f，（3）e，（4）c，（5）d，（6）b |
| C、（1）a，（2）b，（3）e，（4）c，（5）d，（6）f |
| D、（1）a，（2）f，（3）d，（4）c，（5）e，（6）b |
分析：利用幂函数的性质直接推出结果；或利用函数的定义域、值域、单调性推出结果．由题中条件：“n取6个值”，依据幂函数y=xn的性质，在第一、二、三象限内的图象特征可得．
解答：解：根据幂函数y=xn的性质，在第一象限内的图象当n＞0时，n越大，递增速度越快，
故（1）a；（2）f；（3）e，
当n＜0时，|n|越大，曲线越陡峭，
所以（4）c，（5）d，（6）b．
故选B．
故（1）a；（2）f；（3）e，
当n＜0时，|n|越大，曲线越陡峭，
所以（4）c，（5）d，（6）b．
故选B．
点评：本题考查幂函数的图象和性质，考查学生推理能力，是基础题．幂函数是重要的基本初等函数模型之一．学习幂函数重点是掌握幂函数的图形特征，即图象语言，熟记幂函数的图象、性质，把握幂函数的关键点（1，1）和利用直线y=x来刻画其它幂函数在第一象限的凸向．
练习册系列答案
名校课堂系列答案
相关题目
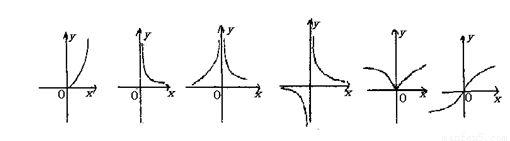
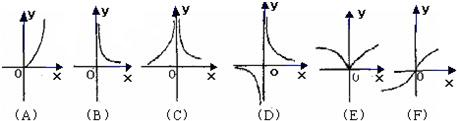
下面六个幂函数的图象如图所示，试建立函数与图象之间的对应关系．（ ）
（1）y=x
；（2）y=x
；（3）y=x
；（4）y=x-2；（5）y=x-3；（6）y=x-
．
（1）y=x
| 3 |
| 2 |
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 2 |
| A、（1）?（A），（2）?（F），（3）?（E），（4）?（C），（5）?（D），（6）?（B） |
| B、（1）?（B），（2）?（E），（3）?（C），（4）?（D），（5）?（A），（6）?（F） |
| C、（1）?（A），（2）?（E），（3）?（B），（4）?（D），（5）?（C），（6）?（F） |
| D、（1）?（B），（2）?（F），（3）?（A），（4）?（C），（5）?（D），（6）?（E） |
