题目内容
已知:tan10°tan20°+tan20°tan60°+tan60°tan10°=1,tan15°tan25°+tan25°tan50°+tan50°tan15°=1,
tan20°tan30°+tan30°tan40°+tan40°tan20°=1,…,
(1)分析上面各式的特点,写出一个能反映此特点的等式(你认为正确的就可以);
(2)写出能反映此特点的一般的等式,并加以证明.
【答案】分析:(1)由题意得,式子中共有三个角,最大角与最小角的和与另一个角互余,得到答案为tan5°•tan10°+tan10°•tan75°+tan75°•tan5°=1.
(2)分析上面各式的特点,写出能反映此特点的一般的等式:
解答:解:解:(1)你认为正确的就可以,
如:tan5°•tan10°+tan10°•tan75°+tan75°•tan5°=1(不唯一);
(2) ,证明如下:
,证明如下:
∵tanαtanβ+tanβtanγ+tanγtanα
=tanβ(tanα+tanγ)+tanγtanα
=tanβtan(α+γ)(1-tanαtanγ)+tanγtanα
=(1-tanαtanγ)+tanγtanα
=1.
点评:本题考查类比推理、两角和的正切公式的变形 tanα+tanβ=tan(α+β )•(1-tanα•tanβ) 的应用,以及互余的两个角的正切值等于1.
(2)分析上面各式的特点,写出能反映此特点的一般的等式:

解答:解:解:(1)你认为正确的就可以,
如:tan5°•tan10°+tan10°•tan75°+tan75°•tan5°=1(不唯一);
(2)
 ,证明如下:
,证明如下:∵tanαtanβ+tanβtanγ+tanγtanα
=tanβ(tanα+tanγ)+tanγtanα
=tanβtan(α+γ)(1-tanαtanγ)+tanγtanα
=(1-tanαtanγ)+tanγtanα
=1.
点评:本题考查类比推理、两角和的正切公式的变形 tanα+tanβ=tan(α+β )•(1-tanα•tanβ) 的应用,以及互余的两个角的正切值等于1.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案
相关题目
若已知tan10°=a,求tan110°的值,那么在以下四个答案:①
;②
;③
④
中,正确的是( )
a+
| ||
1-
|
a+
| ||
|
| a2-1 |
| 2a |
| 2 |
| 1-a2 |
| A、①和③ | B、①和④ |
| C、②和③ | D、②和④ |
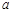 ,求tan110°的值,那么在以下四个答案:
,求tan110°的值,那么在以下四个答案: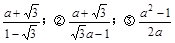 ④
④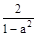 中,正确的是( )
中,正确的是( )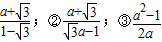 ④
④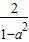 中,正确的是( )
中,正确的是( )