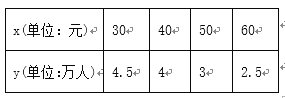
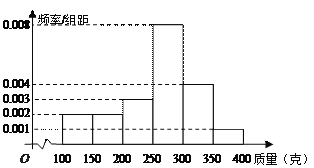
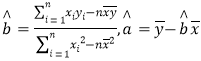题目内容
【题目】已知函数f(x)=sin2x+acosx+x在点x= ![]() 处取得极值.
处取得极值.
(1)求实数a的值;
(2)当x∈[﹣ ![]() ,
, ![]() ]时,求函数f(x)的最大值.
]时,求函数f(x)的最大值.
【答案】
(1)解:f(x)=sin2x+acosx+x,
f′(x)=2cos2x﹣asinx+1,
f′( ![]() )=2cos
)=2cos ![]() ﹣asin
﹣asin ![]() +1=0,
+1=0,
解得:a=4
(2)解:由(1)得:f(x)=sin2x+4cosx+x,
f′(x)=2cos2x﹣4sinx+1=2﹣4sin2x﹣4sinx+1=﹣(2sinx+1)2+4,
令f′(x)>0,解得:﹣ ![]() <x<
<x< ![]() 或
或 ![]() <x<
<x< ![]() ,
,
令f′(x)<0,解得: ![]() <x<
<x< ![]() ,
,
∴f(x)在[﹣ ![]() ,
, ![]() )递增,在(
)递增,在( ![]() ,
, ![]() )递减,在(
)递减,在( ![]() ,
, ![]() )递增,
)递增,
∴f(x)的最大值是f( ![]() )或f(
)或f( ![]() ),
),
而f( ![]() )=
)= ![]() ﹣2+
﹣2+ ![]() <f(
<f( ![]() )=
)= ![]() +
+ ![]() ,
,
故f(x)的最大值是f( ![]() )=
)= ![]() +
+ ![]()
【解析】(1)求出函数的导数,根据f′( ![]() )=0,求出a的值即可;(2)求出函数的导数,解关于导函数的不等式,求出函数的单调区间,从而求出函数的最大值即可.
)=0,求出a的值即可;(2)求出函数的导数,解关于导函数的不等式,求出函数的单调区间,从而求出函数的最大值即可.
【考点精析】关于本题考查的利用导数研究函数的单调性和函数的最大(小)值与导数,需要了解一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减;求函数
在这个区间单调递减;求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值才能得出正确答案.
比较,其中最大的是一个最大值,最小的是最小值才能得出正确答案.

练习册系列答案
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目