题目内容
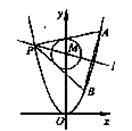
已知抛物线C1:x2=y,圆C2:x2+(y-4)2=1的圆心为点M
(1)求点M到抛物线C1的准线的距离;
(2)已知点P是抛物线C1上一点(异于原点),过点P作圆C2的两条切线,交抛物线C1于A,B两点,若过M,P两点的直线l垂直于AB,求直线l的方程

(1)求点M到抛物线C1的准线的距离;
(2)已知点P是抛物线C1上一点(异于原点),过点P作圆C2的两条切线,交抛物线C1于A,B两点,若过M,P两点的直线l垂直于AB,求直线l的方程
(1) 
(2)见解析;

(2)见解析;
(1)由题意可知,抛物线的准线方程为:y=- 所以圆心M(0,4)到准线的距离是
所以圆心M(0,4)到准线的距离是
(2) 设P(x0,x02),A(x1,x12),B(x2,x22),
则由题意得x0≠0,x0≠±1,x1≠x2,
设过点P的圆C2的切线方程为y-x02=k(x-x0),
即kx-y-kx0 +x02=0 ①
则 =1
=1 ( x02-1)k2+2 x0(4-x02)k+( x02-4)2-1=0,
( x02-1)k2+2 x0(4-x02)k+( x02-4)2-1=0,
设PA,PB的斜率为k1,k2(k1≠k2),则k1,k2是上述方程的两根,所以
k1+k2= ,k1·k2=
,k1·k2=
将①代入x2=y得x2 –kx+kx0-x02=0由于x0是此方程的根,点A或B是过点P作圆C2的两条切线与抛物线C1相交的交点
故,x0+x1=k1,x0+x2=k2 x1=k1-x0,x2=k2- x0
x1=k1-x0,x2=k2- x0
所以kAB= = x1+x2= k1+k2-2x0=
= x1+x2= k1+k2-2x0= -2x0
-2x0
又KMP=
∵MP⊥AB
∴kAB·KMP=[ -2x0]·(
-2x0]·( )=-1,
)=-1,

 ·
· =-1,解
=-1,解 
∴即点P的坐标为(± ,
, ),KMP=
),KMP= =
=
所以直线l的方程为y=± x+4
x+4
 所以圆心M(0,4)到准线的距离是
所以圆心M(0,4)到准线的距离是
(2) 设P(x0,x02),A(x1,x12),B(x2,x22),
则由题意得x0≠0,x0≠±1,x1≠x2,
设过点P的圆C2的切线方程为y-x02=k(x-x0),
即kx-y-kx0 +x02=0 ①
则
 =1
=1 ( x02-1)k2+2 x0(4-x02)k+( x02-4)2-1=0,
( x02-1)k2+2 x0(4-x02)k+( x02-4)2-1=0,设PA,PB的斜率为k1,k2(k1≠k2),则k1,k2是上述方程的两根,所以
k1+k2=
 ,k1·k2=
,k1·k2=
将①代入x2=y得x2 –kx+kx0-x02=0由于x0是此方程的根,点A或B是过点P作圆C2的两条切线与抛物线C1相交的交点
故,x0+x1=k1,x0+x2=k2
 x1=k1-x0,x2=k2- x0
x1=k1-x0,x2=k2- x0所以kAB=
 = x1+x2= k1+k2-2x0=
= x1+x2= k1+k2-2x0= -2x0
-2x0又KMP=

∵MP⊥AB
∴kAB·KMP=[
 -2x0]·(
-2x0]·( )=-1,
)=-1,
 ·
· =-1,解
=-1,解 
∴即点P的坐标为(±
 ,
, ),KMP=
),KMP= =
=
所以直线l的方程为y=±
 x+4
x+4
练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目
 中,已知动点
中,已知动点 到点
到点 的距离为
的距离为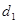 ,到
,到 轴的距离为
轴的距离为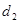 ,且
,且 .
.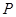 的轨迹
的轨迹 的方程;
的方程;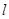 斜率为1且过点
斜率为1且过点 ,其与轨迹
,其与轨迹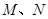 ,求
,求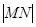 的值.
的值. ,4),则|PA|+|PM|的最小值是
,4),则|PA|+|PM|的最小值是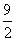
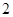 米时,量得水面宽为
米时,量得水面宽为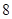 米.则水面升高
米.则水面升高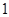 米后,水面
米后,水面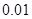 米).
米).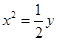 的焦点到准线的距离是( )
的焦点到准线的距离是( )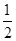
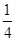
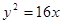 的准线为( )
的准线为( )