题目内容
[例] 已知函数
当
时，求函数
的最小值；
在区间
上的最小值为
。
解析:
当时，
，
。在区间上为增函数。
在区间上的最小值为。
对于函数
若
，则优先考虑用均值不等式求最小值，但要注意等号是否成立，否则会得到
而认为其最小值为
，但实际上，要取得等号，必须使得
，这时
所以，用均值不等式来求最值时，必须注意：一正、二定、三相等，缺一不可。其次,不等式恒成立问题常转化为求函数的最值。本题考查求函数的最小值的三种通法：利用均值不等式，利用函数单调性，二次函数的配方法，考查不等式恒成立问题以及转化化归思想；
练习册系列答案
相关题目
满足：对于任意实数
，都有
恒成立，且当
时，
恒成立；
的值，并例举满足题设条件的一个特殊的具体函数；
在R上的单调性，并加以证明；
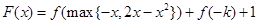(其中
)有三个零点
,求
的取值范围.