Question

3．平面直角坐标系xOy中，O为坐标原点．定义P（x₁，y₁）、Q（x₂，y₂）两点之间的“直角距离”为d（P，Q）=|x₁-x₂|+|y₁-y₂|，已知点B（1，0），点M是直线kx-y+k+3=0（k≥1）上的动点，d（B，M）的最小值为2+$\frac{3}{k}$．

Answer 1

分析 由题意易得d（B，M）=|x₁-x₂|+|y₁-y₂|=|x-1|+|kx+k+3|=|x-1|+k|x+1+$\frac{3}{k}$|，化为分段函数，作图象可得．

解答 解：∵B（1，0），点M为直线kx-y+k+3=0（k≥1）上动点，
设M（x，y），则d（B，M）=|x₁-x₂|+|y₁-y₂|=|x-1|+|y|
=|x-1|+|kx+k+3|=|x-1|+k|x+1+$\frac{3}{k}$|=$\left\{\begin{array}{l}{（k+1）x+k+2，x≥1}\\{（k-1）x+k+4，-（1+\frac{3}{k}）＜x＜1}\\{-（k+1）-k-2，x≤-（1+\frac{3}{k}）}\end{array}\right.$，
作出函数的图象可得当x=-（1+$\frac{3}{k}$）时，d（B，M）的最小值2+$\frac{3}{k}$
故答案为：2+$\frac{3}{k}$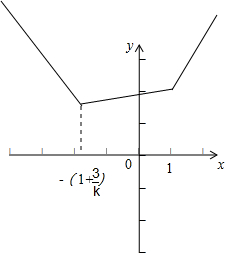

点评 本题考查最值的求解，涉及分段函数和直线的作法，数形结合是解决问题的关键，属中档题．