题目内容
对于函数f(x),在使f(x)≤M恒成立的所有常数M中,我们把M中的最小值称为函数f(x)的“上确界”.已知函数f(x)= +a(x∈[-2,2])是奇函数,则f(x)的上确界为
+a(x∈[-2,2])是奇函数,则f(x)的上确界为
- A.2
- B.

- C.1
- D.

C
分析:首先根据函数是奇函数求出a=-1,然后将函数化成f(x)=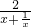 ,再根据均值不等式求出函数的最小值,即可得出答案.
,再根据均值不等式求出函数的最小值,即可得出答案.
解答:∵函数f(x)= +a(x∈[-2,2])是奇函数
+a(x∈[-2,2])是奇函数
∴f(0)=0
∴a=-1
f(x)= -1=
-1=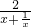
∵x+ ≥2
≥2
∴f(x)= -1=
-1=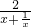 ≤1
≤1
∴f(x)的上确界为1
故选C.
点评:本题考查了函数的最值以及奇函数的特点,解题的关键是根据奇函数求出a的值,属于中档题.
分析:首先根据函数是奇函数求出a=-1,然后将函数化成f(x)=
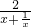 ,再根据均值不等式求出函数的最小值,即可得出答案.
,再根据均值不等式求出函数的最小值,即可得出答案.解答:∵函数f(x)=
 +a(x∈[-2,2])是奇函数
+a(x∈[-2,2])是奇函数∴f(0)=0
∴a=-1
f(x)=
 -1=
-1=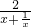
∵x+
 ≥2
≥2∴f(x)=
 -1=
-1=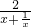 ≤1
≤1∴f(x)的上确界为1
故选C.
点评:本题考查了函数的最值以及奇函数的特点,解题的关键是根据奇函数求出a的值,属于中档题.

练习册系列答案
相关题目