题目内容
已知直线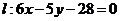 与椭圆
与椭圆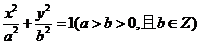 交于
交于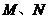 两点,
两点,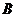 是椭圆的上顶点,
是椭圆的上顶点,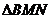 的重心恰为椭圆的右焦点
的重心恰为椭圆的右焦点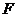 ,(1)求椭圆的方程;(2)是否存在斜率
,(1)求椭圆的方程;(2)是否存在斜率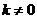 的直线
的直线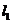 ,使
,使 与该椭圆的两交点
与该椭圆的两交点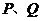 满足
满足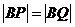 ?若存在,求出
?若存在,求出 在
在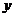 轴上截距的取值范围;若不存在,说明理由.
轴上截距的取值范围;若不存在,说明理由.
设
(1)





点差法: ,
,
因为中点在直线上,所以
解得 或
或  (舍)椭圆方程为
(舍)椭圆方程为
(2)假设存在满足条件的直线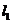 :
: ,
, ,
, 中点为
中点为

 在
在 中垂线上,
中垂线上,




 ,整理得
,整理得 ,
,

当 时,
时, ,
,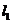 与椭圆无交点,不存在满足条件的直线
与椭圆无交点,不存在满足条件的直线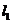

练习册系列答案
相关题目
 中,内角
中,内角 的对边分别是
的对边分别是 ,若
,若 ,
, ,则
,则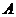 ( )
( ) B.
B. C.
C. D.
D. 
 ,则
,则 的取值范围是( )
的取值范围是( ) B.
B. C.
C. D.
D.
 ,则直线
,则直线 被圆
被圆 所截得的弦长为 ( )
所截得的弦长为 ( ) B. 1 C.
B. 1 C. D.
D.
 的左,右焦点分别为
的左,右焦点分别为 ,点
,点 在双曲线的右支上,且
在双曲线的右支上,且 ,则此双曲线的离心率
,则此双曲线的离心率 的最大值为_____________.
的最大值为_____________.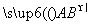 +
+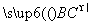 +
+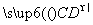 +
+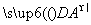 =
=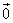 ;
;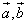 共线,则
共线,则 与
与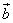 所在直线平行
所在直线平行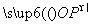 =x
=x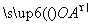 +y
+y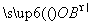 +z
+z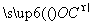 (其中x、y、z∈R),则P、A、B、C四点共面.
(其中x、y、z∈R),则P、A、B、C四点共面. 与双曲线
与双曲线 只有一个公共点,则
只有一个公共点,则 的值有
的值有 个 B.
个 B. 个 C.
个 C. 个 D.无数多个
个 D.无数多个 在
在 上单调递增,则实数
上单调递增,则实数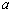 的取值范围( )
的取值范围( )



 ,给出下列三个结论:
,给出下列三个结论: >
> ;②
;②  <
< ; ③
; ③  ,
,